
【题目】阅读:对于两个不等的非零实数![]() 、
、![]() ,若分式
,若分式![]() 的值为零,则
的值为零,则![]() 或
或![]() .又因为
.又因为![]() ,所以关于
,所以关于![]() 的方程
的方程![]() 有两个解,分别为
有两个解,分别为![]() ,
,![]() .
.
应用上面的结论解答下列问题:
(1)方程![]() 的两个解分别为
的两个解分别为![]() ,
,![]() ,则
,则![]() _________,
_________,![]() _________;
_________;
(2)方程![]() 的两个解分别为
的两个解分别为![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)关于![]() 的方程
的方程![]() 的两个解分别为
的两个解分别为![]() ,求
,求![]() 的值.
的值.
【答案】(1)6,1;(2)161;(3)1.
【解析】
(1)根据材料可得:p=2×3=6,q=2+3=1,计算出结果;
(2)根据材料得到ab=-2,a+b=3,再把![]() 变形求解代入求解;
变形求解代入求解;
(3)将原方程变形后变为:2x+1+![]() =2n+1,未知数变为整体2x+1,根据材料中的结论可得:x1=
=2n+1,未知数变为整体2x+1,根据材料中的结论可得:x1=![]() ,x2=
,x2=![]() ,代入所求式子可得结论.
,代入所求式子可得结论.
(1)∵方程![]() 的两个解分别为
的两个解分别为![]() ,
,![]() ,
,
∴p=2×3=6,q=2+3=1,
故答案为:6,1;
(2)∵方程![]() 的两个解分别为
的两个解分别为![]() ,
,![]() ,
,
∴ ab=-2,a+b=3,
∴(a+b)2= a2+b2+2ab=9
故a2+b2=9-2ab=13
∴(a2+b2)2= a4+b4+2a2b2=169
∴a4+b4=169-2a2b2=169-2×(ab)2=169-8=161;
(3)∵![]()
∴2x+1+![]() =2n+1,
=2n+1,
2x+1+![]() =(n+2)+(n1),
=(n+2)+(n1),
∴2x+1=n+2或2x+1=n1,
x=![]() 或
或![]() ,
,
∵x1<x2,
∴x1=![]() ,x2=
,x2=![]() ,
,
∴![]() =
=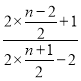 =
=![]() =1.
=1.


科目:初中数学 来源: 题型:
【题目】已知如图![]() ,在以
,在以![]() 为原点的平面直角坐标系中,抛物线
为原点的平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,直线
,直线![]() 过点
过点![]() 且平行于
且平行于![]() 轴,
轴,![]() ,
,
![]() 求抛物线对应的二次函数的解析式;
求抛物线对应的二次函数的解析式;
![]() 若
若![]() 为抛物线
为抛物线![]() 上一动点,是否存在直线
上一动点,是否存在直线![]() 使得点
使得点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长恒相等?若存在,求出此时
的长恒相等?若存在,求出此时![]() 的值;
的值;
![]() 如图
如图![]() ,若
,若![]() 、
、![]() 为上述抛物线上的两个动点,且
为上述抛物线上的两个动点,且![]() ,线段
,线段![]() 的中点为
的中点为![]() ,求点
,求点![]() 纵坐标的最小值.
纵坐标的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
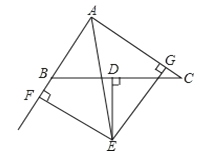
【题目】如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
求证:(1)BF=CG;(2)AF=![]() (AB+AC).
(AB+AC).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船以每小时40海里的速度在海面上航行,当该轮船行驶到B处时,发现灯塔C在它的东北方向,轮船继续向北航行,30分钟后到达A处,此时发现灯塔C在它的北偏东75°方向上,求此时轮船与灯塔C的距离.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步促进“美丽校园”创建工作,某校团委计划对八年级五个班的文化建设进行检查,每天随机抽查一个班级,第一天从五个班级随机抽取一个进行检查,第二天从剩余的四个班级再随机抽取一个进行检查,第三天从剩余的三个班级再随机抽取一个进行检查…,以此类推,直到检查完五个班级为止,且每个班级被选中的机会均等
(1)第一天,八(1)班没有被选中的概率是 ;
(2)利用网状图或列表的方法,求前两天八(1)班被选中的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2+bx+c的图像与x 轴交于A、B两点,与y轴交于点C,OB=OC.点D在函数图像上,CD//x轴,且CD=2,直线l 是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c 的值;
(2)如图①,连接BE,线段OC 上的点F 关于直线l 的对称点F′ 恰好在线段BE上,求点F的坐标;
(3)如图②,动点P在线段OB上,过点P 作x 轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.

图 ① 图②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com