
【题目】探究思考:(本题直接填空,不必写出解题过程)
问题:在数轴上,点A表示的数为![]() ,则到点A的距离等于3的点所表示的数是 ;
,则到点A的距离等于3的点所表示的数是 ;
变式思考一:如图1,在数轴上有六个点A、B、C、D、E、F,且相邻两点间距离相等,若点A表示的数是![]() ,点F表示的数为11,则与点C表示的数最近的整数是 ;
,点F表示的数为11,则与点C表示的数最近的整数是 ;
![]()
变式思考二:已知数轴上有A、B、C三点,分别代表![]() ,电子蚂蚁从A向点C方向以4个单位/秒的速度爬行.则爬行到 秒时,电子蚂蚁到A、B、C的距离和为40个单位.
,电子蚂蚁从A向点C方向以4个单位/秒的速度爬行.则爬行到 秒时,电子蚂蚁到A、B、C的距离和为40个单位.
【答案】问题:-4或2;变式思考一:1;变式思考二:2或5
【解析】
问题:数轴上若点A表示的数是-1,另一点与点A的距离为3,则分这点在点A的左边和右边两种情况讨论可得;
变式思考一:先求出相邻两个字母的间距,然后求到点C表示的数,即可得到距离C最近的整数;
变式思考二:设y秒后甲到A,B,C三点的距离之和为40个单位,分电子蚂蚁应位于AB或BC之间两种情况讨论即可求解.
解:问题:分两种情况:①这个点在A左边时,这个点表示的数是-1-3=-4;②这个点在A右边时,这个点表示的数是-1+3=2;
故答案为:-4或2;
变式思考一:相邻两个字母的间距=[11-(-5)]÷5=3.2,所以点C表示的数=-5+3.2×2=1.4,
则与点C表示的数最近的整数是1,
故答案为:1;
变式思考二:设y秒后甲到A,B,C三点的距离之和为40个单位,
B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C点距A、B的距离为34+20=54>40,故甲应为于AB或BC之间.
①AB之间时:4y+(14-4y)+(14-4y+20)=40
解得y=2;
②BC之间时:4y+(4y-14)+(34-4y)=40,
解得y=5.
故答案为:2或5;


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;

(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张对边互相平行的纸条沿EF折叠,若∠EFB=32°,则①∠C′EF=32°;②∠AEC=148°;③∠BGE=64°;④∠BFD=116°;则下列结论正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
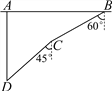
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠B=90°,点P从点A出发,沿A→B→C以1cm/s的速度运动.设△APC的面积为s(m),点P的运动时间为t(s),变量S与t之间的关系如图2所示,则在运动过程中,S的最大值是______.
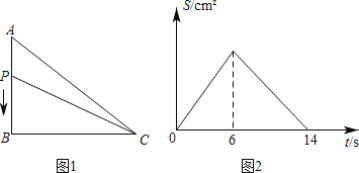
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式ab=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,
,给出定义如下:我们称使等式ab=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,![]() ),(5,
),(5,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(2,1),(3,![]() )中是“共生有理数对”的是_____________;
)中是“共生有理数对”的是_____________;
(2)若(m,n)是“共生有理数对”,则(n,m)_____“共生有理数对”(填“是”或“不是”);说明理由;
(3)若(a,3)是“共生有理数对”,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016齐齐哈尔)有一科技小组进行机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上.甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走.如图是甲、乙两机器人之间的距离y(米)与它们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是________米,甲机器人前2分钟的速度为______米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段![]() 轴,则此段时间,甲机器人的速度为________米/分;
轴,则此段时间,甲机器人的速度为________米/分;
(4)求A、C两点之间的距离;
(5)直接写出两机器人出发多长时间相距28米.
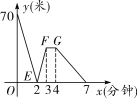
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com