
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式ab=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,
,给出定义如下:我们称使等式ab=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,![]() ),(5,
),(5,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(2,1),(3,![]() )中是“共生有理数对”的是_____________;
)中是“共生有理数对”的是_____________;
(2)若(m,n)是“共生有理数对”,则(n,m)_____“共生有理数对”(填“是”或“不是”);说明理由;
(3)若(a,3)是“共生有理数对”,求a的值.
【答案】(1)(3,![]() );(2)是;(3)a=﹣2.
);(2)是;(3)a=﹣2.
【解析】
(1)根据“共生有理数对”的定义即可判断;
(2)根据“共生有理数对”的定义即可判断;
(3)根据“共生有理数对”的定义,构建方程即可解决问题.
(1)﹣2﹣1=﹣3,﹣2×1+1=1,∴﹣2﹣1≠﹣2×1+1,∴(﹣2,1)不是“共生有理数对”.
∵3![]() ,3
,3![]() 1
1![]() ,∴3
,∴3![]() 3
3![]() 1,∴(3,
1,∴(3,![]() )是“共生有理数对”;
)是“共生有理数对”;
(2)是.
理由:﹣m﹣(﹣n)=﹣n+m,﹣n(﹣m)+1=mn+1.
∵(m,n)是“共生有理数对”,∴m﹣n=mn+1,∴﹣n+m=mn+1,∴(﹣n,﹣m)是“共生有理数对”.
故答案为:是.
(3)由题意得:a﹣3=3a+1,解得:a=﹣2.


科目:初中数学 来源: 题型:
【题目】探究思考:(本题直接填空,不必写出解题过程)
问题:在数轴上,点A表示的数为![]() ,则到点A的距离等于3的点所表示的数是 ;
,则到点A的距离等于3的点所表示的数是 ;
变式思考一:如图1,在数轴上有六个点A、B、C、D、E、F,且相邻两点间距离相等,若点A表示的数是![]() ,点F表示的数为11,则与点C表示的数最近的整数是 ;
,点F表示的数为11,则与点C表示的数最近的整数是 ;
![]()
变式思考二:已知数轴上有A、B、C三点,分别代表![]() ,电子蚂蚁从A向点C方向以4个单位/秒的速度爬行.则爬行到 秒时,电子蚂蚁到A、B、C的距离和为40个单位.
,电子蚂蚁从A向点C方向以4个单位/秒的速度爬行.则爬行到 秒时,电子蚂蚁到A、B、C的距离和为40个单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每一个小正方形的边长为1个单位长度.可以利用平面直角坐标系的知识回答以下问题:
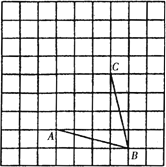
(1)请在所给的网格内画出以线段AB、BC为边的平行四边形ABCD;
(2)填空:平行四边形ABCD的面积等于____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图E是平行四边形![]() 边BC上一点,且
边BC上一点,且![]() ,连接AE,并延长AE与DC的延长线交于点F,
,连接AE,并延长AE与DC的延长线交于点F, ![]() .
.
(1)请判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)求![]() 的各内角的大小.
的各内角的大小.
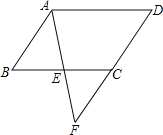
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
计算:(-5)÷![]() ×20.
×20.
解:原式=(-5)÷![]() ×20 (第一步)
×20 (第一步)
=(-5)÷(-1) (第二步)
=-5. (第三步)
(1)上述解题过程中有两处错误:
第一处是第________步,错误的原因是__________________________;
第二处是第________步,错误的原因是_______________________.
(2)把正确的解题过程写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个迷你数独,图中实线划分的区域是一个宫,共有4个宫,每一宫又被虚线分为四个小格.根据图中已经给的提示数字,在其他的空格上填入-1、-2、-3、-4的数字.使-1、-2、-3、-4每个数字在每一行、每一列和每一宫中都只出现一次。则图中点A的位置所填的数字为 ( )

A. -1B. -2C. -3D. -4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民吉姆上星期买进某公司月股票![]() 股,每股
股,每股![]() 元,下表为本周内每日该股的涨跌情况(星期六、日股市休市)(单位:元)
元,下表为本周内每日该股的涨跌情况(星期六、日股市休市)(单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +1.5 | ﹣0.7 | ﹣1.2 | +2 | ﹣1.8 |
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价多少元?最低价是多少元?
(3)已知吉姆买进股票时付了![]() 的手续费,卖出时还需付成交额
的手续费,卖出时还需付成交额![]() 的手续费和的
的手续费和的![]() 交易税,如果吉姆在星期五收盘前将全部股票卖出,他的收益情况如何?
交易税,如果吉姆在星期五收盘前将全部股票卖出,他的收益情况如何?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com