【题目】如图，在等边
中，
是过点
的一条直线，点
关于直线的对称点为
，连接
，
，
，其中，分别交直线于点
，
.
（1）若
（
），请用
的代数式表示
；
（2）求证：
.
【答案】（1）
；（2）详见解析.
【解析】
（1）由对称的性质可得BH是CD的垂直平分线，从而有
，再根据等腰三角形的三线合一性质可得BH是
的角平分线，从而可得的度数，利用等边三角形的性质可得
的度数和
是等腰三角形，最后根据等腰三角形的性质求解即可；
（2）如图（见解析），在
上截取
使
，连接
，由题（1）的结论和直角三角形的性质求出
，从而可得
是等边三角形，再利用外角性质推出
，然后根据三角形全等的判定定理得
，由此可得
，最后根据线段的和差、等量代换即可证.
（1）∵点
与点
关于
对称
∴是
的垂直平分线
∴
是等腰三角形
是的角平分线（等腰三角形的三线合一性质）
∵
∴
∵
是等边三角形
∴
∴
∵
是等腰三角形
∴
；
（2）如图，在上截取使，连接
∵
，
∴
∴
∴
∵
∴是等边三角形
∴
,
∵
∴
∵
∴
∴
∵
∴
.
科目：初中数学 来源： 题型：
【题目】如图1，在矩形ABCD中，点A(1，1)，B(3，1)，C(3，2)，反比例函数y=
(x>0)的图象经过点D，且与AB相交于点E,
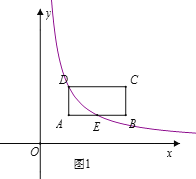
（1）求反比例函数的解析式；
（2）过点C、E作直线，求直线CE的解析式；
（3）如图2，将矩形ABCD沿直线CE平移，使得点C与点E重合，求线段BD扫过的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知如图，
是边长为
的正
的边
上一点，
交
于
，
交
于
，设
．
求
的面积
与
的函数关系式和自变量的取值范围．
当为何值时，的面积最大，最大面积是多少？
若
与由、、三点组成的三角形相似，求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC各顶点的坐标分别为A（-3，2），B（-4，-3），C（-1，-1）
（1）画出△ABC，并画出△ABC关于y轴对称的△A1B1C1，并写出A的对应点A1的坐标.
（2）尺规作图，∠A的角平分线AD，交BC于点D（保留作图痕迹，不写作法）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小慧家与文具店相距720米，小慧从家出发，匀速步行12分钟来到文具店，买文具用时4分钟，因家中有事，沿原路匀速跑步返回家中，用时6分钟.
（1）小慧返回家中的速度比去文具店的速度快 米/分钟；
（2）请你画出这个过程中，小慧离家的距离
与时间
的函数图象；
（3）求小慧从家出发后经过多少分钟与她家距离为480米.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）．
（1）将△ABC向下平移5个单位后得到△A1B1C1，请画出△A1B1C1；
（2）将△ABC绕原点O逆时针旋转90°后得到△A2B2C2，请画出△A2B2C2；
（3）判断以O，A1，B为顶点的三角形的形状．（无须说明理由）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：二次函数图象的顶点坐标是（3，5），且抛物线经过点A（1，3）．
（1）求此抛物线的表达式；
（2）如果点A关于该抛物线对称轴的对称点是B点，且抛物线与y轴的交点是C点，求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,四 边形OABC是矩形,点A、C在坐标轴上，△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在X轴上，直线BD交Y轴于点F,交OE于点H,线段BC、OC的长是方程x2-6x+8=0的两个根，且OC＞BC.
（1）求直线BD的解析式.
（2）求 △OFH的面积.
（3）点M在坐标轴上，平面内是否存在点N，使以点D、F、M、N为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】期末，学校为了调查这学期学生课外阅读情况，随机抽样调查了一部分学生阅读课外书的本数，并将收集到的数据整理成如图的统计图．
（1）这次一共调查的学生人数是_______人；
（2）所调查学生读书本数的众数是_______本，中位数是_______本．
（3）若该校有800名学生，请你估计该校学生这学期读书总数是多少本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com