
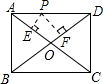
 如图,P是矩形的边AD上一个动点,AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是2.4.
如图,P是矩形的边AD上一个动点,AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是2.4. 分析 首先连接OP,由矩形的两条边AB、BC的长分别为3和4,可求得OA=OD=2.5,△AOD的面积,然后由S△AOD=S△AOP+S△DOP=$\frac{1}{2}$OA•PE+OD•PF求得答案.
解答 解:连接OP,
∵矩形的两条边AB、BC的长分别为3和4,
∴S矩形ABCD=AB•BC=12,OA=OC,OB=OD,AC=BD=5,
∴OA=OD=2.5,
∴S△ACD=$\frac{1}{2}$S矩形ABCD=6,
∴S△AOD=$\frac{1}{2}$S△ACD=3,
∵S△AOD=S△AOP+S△DOP=$\frac{1}{2}$OA•PE+$\frac{1}{2}$OD•PF=$\frac{1}{2}$×2.5×PE+$\frac{1}{2}$×2.5×PF=$\frac{5}{4}$(PE+PF)=3,
解得:PE+PF=2.4.
故答案为:2.4.
点评 此题考查了矩形的性质以及三角形面积问题.此题难度适中,注意掌握辅助线的作法以及掌握整体数学思想的运用是解题的关键.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com