
【题目】甲、乙两车同时分别从 A,B 两处出发,沿直线 AB 作匀速运动,同时到达C 处,B 在 AC 上,甲的速度是乙的速度的1.5 倍,设 t(分)后甲、 乙两遥控车与 B 处的距离分别为 d1,d2,且 d1,d2 与出发时间 t 的函数关系如图,那么在两车相遇前,两车与 B 点的距离相等时,t 的值为( )
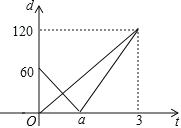
A.0.4B.0.5C.0.6D.1
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】已知,如图在ABCD中,点E为AB上一点,连接CE、DE,且CE⊥AB,CE=AB,点F为BC上一点,连接DF交CE于点G,∠CGD=∠B;

(1)若CG=2,AD=3,求GE的长;
(2)若CF=![]() DE,求证:AD=CG+BE.
DE,求证:AD=CG+BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,A(2,4),B(4,1),C(-3,4)

(1)平移线段AB到线段CD,使点A与点C重合,写出点D的坐标.
(2)直接写出线段AB平移至线段CD处所扫过的面积.
(3)平移线段AB,使其两端点都在坐标轴上,则点A的坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买![]() 、
、![]() 两种型号的机器人搬运材料,已知
两种型号的机器人搬运材料,已知![]() 型机器人比
型机器人比![]() 型机器人每小时多搬运
型机器人每小时多搬运![]() 材料,且
材料,且![]() 型机器人搬运
型机器人搬运![]() 的材料所用的时间与
的材料所用的时间与![]() 型机器人搬运
型机器人搬运![]() 材料所用的时间相同.
材料所用的时间相同.
(1)求![]() 、
、![]() 两种型号的机器人每小时分别搬运多少材料?
两种型号的机器人每小时分别搬运多少材料?
(2)该公司计划采购![]() 、
、![]() 两种型号的机器人共
两种型号的机器人共![]() 台,要求每小时搬运的材料不得少于
台,要求每小时搬运的材料不得少于![]() ,则至少购进
,则至少购进![]() 型机器人多少台?
型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) |
|
销售玩具获得利润w(元) |
|
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,并解决问题.
分式方程的增根:解分式方程时可能会产生增根,原因是什么呢?事实上,解分式方程时产生增根,主要是在去分母这一步造成的.根据等式的基本性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.但是,当等式两边同乘0时,就会出现![]() 的特殊情况.因此,解方程时,方程左右两边不能同乘0.而去分母时会在方程左右两边同乘公分母,此时无法知道所乘的公分母的值是否为0,于是,未知数的取值范围可能就扩大了.如果去分母后得到的整式方程的根使所乘的公分母值为0,此根即为增根,增根是整式方程的根,但不是原分式方程的根.所以解分式方程必须验根.请根据阅读材料解决问题:
的特殊情况.因此,解方程时,方程左右两边不能同乘0.而去分母时会在方程左右两边同乘公分母,此时无法知道所乘的公分母的值是否为0,于是,未知数的取值范围可能就扩大了.如果去分母后得到的整式方程的根使所乘的公分母值为0,此根即为增根,增根是整式方程的根,但不是原分式方程的根.所以解分式方程必须验根.请根据阅读材料解决问题:
(1)若解分式方程![]() 时产生了增根,这个增根是 ;
时产生了增根,这个增根是 ;
(2)小明认为解分式方程![]() 时,不会产生增根,请你直接写出原因;
时,不会产生增根,请你直接写出原因;
(3)解方程![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,E是BC的中点,以点A为中心,把△ABE绕点A顺时针旋转90°,设点E的对应点为F.

(1)画出旋转后的三角形.(尺规作图,保留作图痕迹,不写作法)
(2)求点E运动到点F所经过的路径的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com