
 如图,A为半径18cm的⊙O上的定点,动点P从A出发,以3πcm/s的速发沿圆周按逆时针方向运动,当点P回到A地立即停止运动.
如图,A为半径18cm的⊙O上的定点,动点P从A出发,以3πcm/s的速发沿圆周按逆时针方向运动,当点P回到A地立即停止运动.分析 (1)当∠POA=90°时,点P运动的路程为⊙O周长的$\frac{1}{4}$或$\frac{3}{4}$,所以分两种情况进行分析;
(2)直线BP与⊙O的位置关系是相切,根据已知可证得OP⊥BP,即直线BP与⊙O相切.
解答 解:(1)当∠POA=90°时,根据弧长公式可知点P运动的路程为⊙O周长的$\frac{1}{4}$或$\frac{3}{4}$,
设点P运动的时间为ts;
当点P运动的路程为⊙O周长的$\frac{1}{4}$时,3π•t=$\frac{1}{4}$•2π•18,
解得t=3;
当点P运动的路程为⊙O周长的$\frac{3}{4}$时,3π•t=$\frac{3}{4}$•2π•18,
解得t=9;
∴当∠POA=90°时,点P运动的时间为3s或9s.
(2)解:∵当OP⊥PB时,BP与⊙O相切,
∵AB=OA,OA=OP,
∴OB=2OP,∠OPB=90°;
∴∠B=30°;
∴∠O=60°;
∵OA=9cm,
∴$\widehat{AP}$=$\frac{60•π×9}{180}$=3π,
∴点P运动的距离为3π,
∴当t=1,有BP与⊙O相切.
点评 本题考查的是切线的性质及弧长公式,解答(2)题时要注意过圆外一点有两条直线与圆相切,不要漏解.


科目:初中数学 来源: 题型:解答题
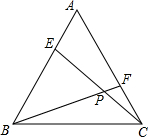 如图,E、F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE、BF交于点P.
如图,E、F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE、BF交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,反比例函数y=$\frac{k}{x}$(≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
如图,反比例函数y=$\frac{k}{x}$(≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com