
【题目】某商品公司为指导某种应季商品的生产和销售,在对历年市场行情和生产情况进行调查基础上,对今年这种商品的市场售价和生产成本进行了预测并提供了两个方面的信息:如图(1)(2).

注:两图中的每个实心黑点所对应的纵坐标分别指相应月份一件商品的售价和成本,生产成本6月份最高;图(1)的图象是线段,图(2)的图象是抛物线.
(1)在3月份出售这种商品,一件商品的利润是多少?
(2)设t月份出售这种商品,一件商品的成本Q(元),求Q关于t的函数解析式.
(3)设t月份出售这种商品,一件商品的利润W(元),求W关于t的函数解析式.
(4)问哪个月出售这种商品,一件商品的利润最大?简单说明理由.
【答案】(1)5元;(2)Q=﹣![]() (t﹣6)2+4=﹣
(t﹣6)2+4=﹣![]() t2+4t﹣8(3)W=
t2+4t﹣8(3)W=![]() (t﹣5)2+
(t﹣5)2+![]() (4)
(4)![]() 元
元
【解析】
试题分析:(1)从图易知3月份每件商品售价6元,成本1元,易求利润;
(2)根据图象特征设解析式为顶点式易求解析式;
(3)根据利润的计算方法,显然需求直线解析式,再求差,
(4)运用函数性质计算利润.
解:(1)每件商品在3月份出售时的利润为5元;
(2)∵抛物线的顶点坐标为(6,4)
∴设抛物线的解析式为Q=a(t﹣6)2+4
∵抛物线过(3,1)点
∴1=a(3﹣6)2+4
解得:a=﹣![]()
∴Q=﹣![]() (t﹣6)2+4=﹣
(t﹣6)2+4=﹣![]() t2+4t﹣8,其中t=3、4、5、6、7;
t2+4t﹣8,其中t=3、4、5、6、7;
(3)设每件商品的售价M(元)与时间t(月)之间的函数关系式为M=kt+b
∵线段过(3,6)、(6,8)两点
∴3k+b=6 6k+b=8
解得:k=![]() ,b=4
,b=4
∴M=![]() t+4,其中t=3、4、5、6、7;
t+4,其中t=3、4、5、6、7;
(4)每件商品的利润W(元)与时间t(月)的函数关系式为
W=M﹣Q=(![]() t+4)﹣(﹣
t+4)﹣(﹣![]() t2+4t﹣8)=
t2+4t﹣8)=![]() t2﹣
t2﹣![]() t+12
t+12
∴W=![]() (t﹣5)2+
(t﹣5)2+![]() ,其中t=3、4、5、6、7
,其中t=3、4、5、6、7
∴当t=3或7时,W的最大值为![]() 元.
元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数![]() 的图象上.那么k的值是 .
的图象上.那么k的值是 .
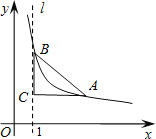
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个口袋中均有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的数值分别为﹣7,﹣1,3,乙袋中的三张卡片上所标的数值分别为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用y表示取出的卡片上标的数值,把x,y分别作为点A的横坐标和纵坐标.
(1)请用列表或画树状图法,表示出点A(x,y)所有可能出现的结果;
(2)求点A在第三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC.M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为 cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动,已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG,设E点移动距离为x(x>0).
(1)△EFG的边长是 (用含有x的代数式表示),当x=2时,点G的位置在 ;
(2)若△EFG与梯形ABCD重叠部分面积是y,求y与x之间的函数关系式;
(3)探究(2)中得到的函数y在x取何值时,存在最大值?并求出最大值.
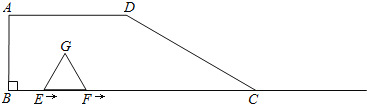
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中真命题的是_____(填写命题序号)
①若a+b>0且ab>0,则a>0且b>0.
②若a>b且ab>0,则a>b>0.
③在同一平面内,垂直于同一直线的两直线平行.
④一个锐角的补角比它的余角小90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】15名同学参加八年级数学竞赛初赛,他们的得分互不相同,按从高分到低分的原则,录取前8名同学参加复赛,现在小聪同学已经知道自己的分数,如果他想知道自己能否进入复赛,那么还需知道所有参赛学生成绩的
A. 平均数B. 中位数C. 众数D. 方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com