
【题目】如图,![]() 为长方形
为长方形![]() 的对角线,将边
的对角线,将边![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处.将边
处.将边![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处。
处。
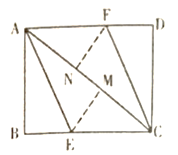
![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 若
若![]() ,求四边形
,求四边形![]() 的面积。
的面积。
【答案】(1)证明过程见解析;(2)四边形![]() 的面积为30.
的面积为30.
【解析】
(1)首先证明△ABE≌△CDF,则DF=BE,然后可得到AF=EC,依据一组对边平行且相等的四边形是平行四边形可证明AECF是平行四边形;
(2)由![]() 可得BC=8,由折叠性质可设BE=EM=x,根据
可得BC=8,由折叠性质可设BE=EM=x,根据![]() ,可以求出x的值,进而求出四边形
,可以求出x的值,进而求出四边形![]() 的面积.
的面积.
(1)证明:∵四边形ABCD为矩形
∴AB=CD,AD∥CB,∠B=∠D=90°,∠BAC=∠DCA
由翻折性质可知:∠EAB=![]() ∠BAC,∠DCF=
∠BAC,∠DCF=![]() ∠DCA
∠DCA
∴∠EAB=∠DCF
在△ABE和△CDF中

∴△ABE≌△CDF
∴BE=DF
∴AF=CE
又AF∥CE
∴四边形AECF是平行四边形.
(2)解:∵![]()
∴BC=8
由翻折性质可知:BE=EM
可设BE=EM=x
![]()
![]()
![]()
且![]()
即:![]()
解得x=3
∴CE=BC-BE=8-3=5
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某班级准备购买一些奖品奖励春季运动会表现突出的同学,奖品分为甲、乙两种,已知,购买一个甲奖品比一个乙奖品多用20元,若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.
(1)求购买一个甲奖品和一个乙奖品各需多少元?
(2)经商谈,商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠,如果该班级需要乙奖品的个数是甲奖品的2倍还多8个,且该班级购买两种奖项的总费用不超过640元,那么该班级最多可购买多少个甲奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按月收费,标准如下:
①若每户月用水不超过![]() ,按
,按![]() 元/
元/![]() 收费;
收费;
②若超过![]() ,但不超过
,但不超过![]() ,则超过的部分按
,则超过的部分按![]() 元/
元/![]() 收费,未超过
收费,未超过![]() 部分按①标准收费;
部分按①标准收费;
③若超过![]() ,超过的部分按
,超过的部分按![]() 元/
元/![]() 收费,未超过
收费,未超过![]() 部分按②标准收费;
部分按②标准收费;
(1)若用水![]() ,应交水费______元;(用含
,应交水费______元;(用含![]() 的式子表示)
的式子表示)
(2)小明家上个月用水![]() ,交水费
,交水费![]() 元,求
元,求![]() 的值;
的值;
(3)在(2)的条件下,小明家七、八两个月共交水费![]() 元,七月份用水
元,七月份用水![]() 超过
超过![]() ,但不足
,但不足![]() ,八月份用水
,八月份用水![]() 超过
超过![]() ,当
,当![]() 均为整数时,求
均为整数时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多边形上或内部的一点与多边形各顶点的连线,可以将多边形分割成若干个小三角形.如图,给出了四边形的三种具体分割方法,分别将四边形分割成了2个、3个、4个小三角形,这样我们就可以借助研究三角形的经验研究四边形了.
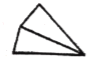
图①被分割成2个小三角形

图②被分割成3个小三角形

图③被分割成4个小三角形
(1)请按照上述三种方法分别将图中的六边形进行分割,并写出每种方法所得到的小三角形的个数:
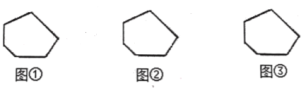
图①被分割成 个小三角形、图②被分割成 个小三角形、图③被分割成 个小三角形;
(2)如果按照上述三种分割方法分别分割![]() 边形,请写出每种方法所得到的小三角形的个数(用含
边形,请写出每种方法所得到的小三角形的个数(用含![]() 的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,
的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,![]() 边形分别可以被分割成 、 、 个小三角形.
边形分别可以被分割成 、 、 个小三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠AFC,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°—∠ABD;④∠BDC=![]() ∠BAC,其中正确的结论有_____________。
∠BAC,其中正确的结论有_____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列![]() 个生产、生活现象中,可用“两点之间线段最短”来解释的是( )
个生产、生活现象中,可用“两点之间线段最短”来解释的是( )
A.用两根钉子就可以把木条固定在墙上
B.植树时,只要选出两棵树的位置,就能确定同一行树所在的直线
C.把弯曲的公路改直,就能缩短路程
D.砌墙时,经常在两个墙角的位置分别插一根木桩拉一条直的参照线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△OA1B1绕点O逆时针旋转90°,得△OA2B2;△OA2B2绕点O逆时针旋转90°,得△OA3B3;△OA3B3绕点O逆时针旋转90°,得△OA4B4;…;若点A1(1,0),B1(1,1),则点B4的坐标是________,点B 2018的坐标是________.
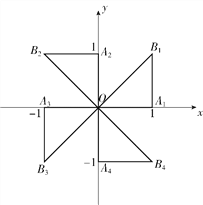
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com