
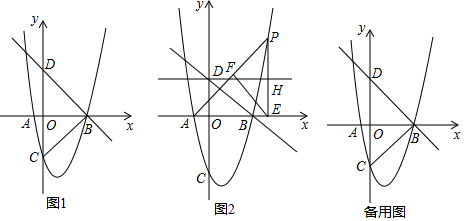
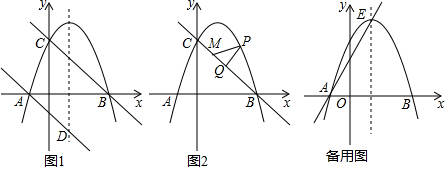
分析 (1)由一次函数图象上点的坐标特征求得点B的坐标,然后把点B的坐标代入函数解析式即可求得k的值;
(2)如答图1,根据垂直的定义和同角的余角相等推知∠PEF=∠PAE.结合矩形DOEH的性质得到:HE=2.所以,根据三角函数的定义推知:$\frac{d}{HE}$=$\frac{PE}{AE}$,即$\frac{d}{2}$=$\frac{(t-1)^{2}-4}{t+1}$.由此得到答案;
(3)利用(2)中求得的函数关系式,矩形的性质和三角函数的定义易得P(4,5).M(2,3).由二次函数图象上点的坐标特征求得N(2,-3),作HW⊥KQ,过R作RL⊥x轴,构建矩形AKWH,全等三角形:△RAM≌△HAN,△ARL≌△AHE.结合坐标与图形的性质得到R(-3,5).由执行直线MRy=$\frac{5}{2}$x-2,直线AK的解析式y=-$\frac{5}{2}$x-$\frac{5}{2}$求得交点R(-$\frac{1}{10}$,$\frac{9}{4}$).
解答 解:(1)在一次函数y=-$\frac{2}{3}$x+2中,令y=0,得:0=-$\frac{2}{3}$x+2,
解得x=3,
∴B(3,0).
令x=0得y=2,
∴D(0,2).
将B(3,0),代入y=(x-1)2+k得:4+k=0,
∴k=-4.
(2)如答图1所示: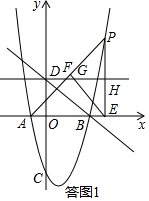
∵PE⊥x轴,EF⊥AP,
∴∠PEA=∠EFA=90°
∵∠PEF+∠FEA=90°,∠PAE+∠FEA=90°
∴∠PEF=∠PAE.
∵DH∥x轴 HE⊥x轴
∴∠HDO=∠DOE=∠PEO=90°
∴四边形DOEH为矩形.
∴HE=2.
∴$\frac{d}{HE}$=$\frac{PE}{AE}$,
∴$\frac{d}{2}$=$\frac{(t-1)^{2}-4}{t+1}$.
∴d=2t-6.(t>3).
(3)∵∠TGH=∠GTE=∠TEH=90°,
∴GHET为矩形.
∴GH=d=ET=2t-6.
∵tan∠MEB=$\frac{3}{2}$,
∴$\frac{MT}{ET}$=$\frac{3}{2}$,
∴MT=3t-9.
∵$\frac{MT}{AT}$=$\frac{PE}{AE}$.
∴$\frac{3(t-3)}{t+1-(2t-6)}$=$\frac{(t-1)^{2}-4}{t+1}$,
解得t=4.
∴P(4,5).
∴AT=AE-ET=t+1-(2t-6)=7-t=3.
∴M(2,3)
把x=2代入y=x2-2x-3中,得N(2,-3)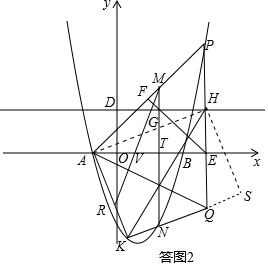
∴MT=TN=AT,∠MAT=90°.
∵∠RAE-∠RMA=45°,
∴∠RAE-45°=∠RMA,
∴∠RAM=∠RMA,
∵S△AKQ=S△HKQ,作HW⊥KQ.
∴AK∥HW,AK=HW,
∴四边形AKWH是矩形,
∴∠RAH=∠HAK=90°,
∴∠RAM=∠HAN.
∵A(-1,0),H(4,2),N(2,-3),
∴AH=HN=$\sqrt{29}$,
∴∠HAN=∠HNA=∠RAM=∠RMA.
又∵AM=AN,
∴△RAM≌△HAN,
∴AR=AH.
过R作RL⊥x轴,
∴∠RLA=∠AEH=90°,
∵∠RAL+∠HAE=90,∠HAE+∠AHE=90,
∴∠RAL=∠AHE,
∴△ARL≌△AHE.
∴RL=AE=5,AL=HE=3
∴R(-3,5).
由∠RAM-∠RMA=45°可知∠RAV=∠RVA,∠RMT=∠HAE,tan∠RMT=tan∠HAE=$\frac{2}{5}$,V($\frac{4}{5}$,0),
直线MR的解析式为y=$\frac{5}{2}$x-2,直线AK的解析式为y=-$\frac{5}{2}$x-$\frac{5}{2}$,
交点R(-$\frac{1}{10}$,$\frac{9}{4}$).
点评 本题考查了二次函数综合题.需要掌握待定系数法求一次函数解析式、二次函数解析式,二次函数图象上点的坐标特征,全等三角形的判定与性质,矩形的判定与性质等知识点,难度较大,注意题中辅助线的作法.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | -ma-m=-m(a-1) | B. | x2-y2=(x-y)2 | C. | a2+3a+9=(a+3)2 | D. | 2x2-2=2(x+1)(x-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:在△ABC中,D、E为AC、AB上的点,BD、CE相交于O,取AB的中点F,联结OF,若AD=$\frac{1}{2}$CD,AE=$\frac{1}{2}$BE
已知:在△ABC中,D、E为AC、AB上的点,BD、CE相交于O,取AB的中点F,联结OF,若AD=$\frac{1}{2}$CD,AE=$\frac{1}{2}$BE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
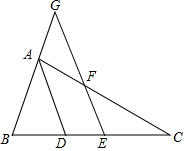 如图,△ABC中,AD平分∠BAC,EF交BA延长线于点G,∠CFE=∠G.
如图,△ABC中,AD平分∠BAC,EF交BA延长线于点G,∠CFE=∠G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
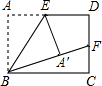 如图,在矩形ABCD中,E、F分别是AD、CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD=2$\sqrt{2}$.
如图,在矩形ABCD中,E、F分别是AD、CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD=2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
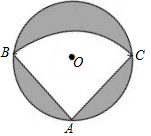 有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.
有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com