
分析 若不能构成三角形,就是这三个动点在一条直线上的时候,在一条直线有三种情况,(1)动点的横坐标相等;(2)动点的纵坐标相等;(3)三点满足一次函数式.
解答 解:(1)动点的横坐标相等时:a=b=c.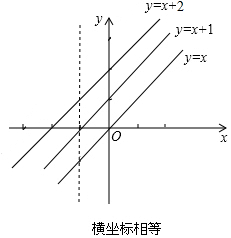
(2)动点的纵坐标相等时:∵y=a,y=b+1,y=c+2,
∴a=b+1=c+2.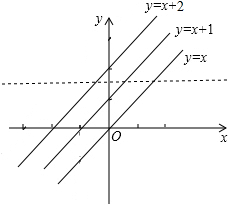
(3)三点满足一次函数式,三点可以表示一次函数的斜率:斜率为函数图象与x轴所形成角的正切值;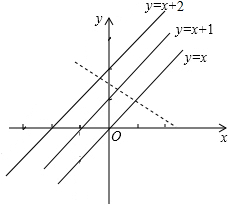
∵三点的坐标为(a,a),(b,b+1),(c,c+2),
∴$\frac{b+1-a}{b-a}$=$\frac{c+2-a}{c-a}$,
1+$\frac{1}{b-a}$=1+$\frac{2}{c-a}$,
∴$\frac{a-c}{a-b}$=2.
故答案为:a=b=c或a=b+1=c+2或$\frac{a-c}{a-b}$=2.
点评 本题考查两条直线相交或平行问题,关键是知道动点满足什么条件时不能构成三角形,即动点在同一直线上时不能三角形,从而可求解.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
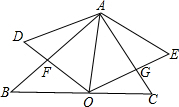 如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.
如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com