
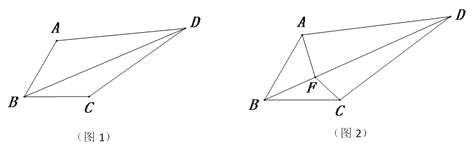
����Ŀ����ͼ1�����ı���ABCD�У�BA=BC����ABC=60�㣬��ADC=30�㣬���ӶԽ���BD��
��1�����߶�CD�Ƶ�C˳ʱ����ת60��õ��߶�CE������AE��
�������ⲹȫͼ1��
�����ж�AE��BD��������ϵ����֤����Ľ��ۣ�
��2���ڣ�1���������£�ֱ��д���߶�DA��DB��DC֮���������ϵ��
��3����ͼ2��F�ǶԽ���BD��һ�㣬�������AFC=150�㣬����FA��FC��̽���߶�FA��FB��FC֮���������ϵ����֤����
���𰸡���1����ͼ�μ�������AE=BD��2���жϣ� ![]() ��3���ж�
��3���ж�![]() ��֤��������
��֤��������
�������������������1���ٸ������⻭ͼ���ɣ�
������AC��֤����BCD�ա�ACE���ɣ�
��2������DE����֤������ADEΪֱ�������Σ��ɹ��ɶ������ɵó����ۣ�
��3�����߶�CF�Ƶ�C˳ʱ����ת60��õ��߶�CE������EF��EA��֤����BCD�ա�ACE��ֱ��������AEF����Ϲ��ɶ�������֤��.
�����������1���ٲ�ȫͼ��,��ͼ1
���ж�: AE=BD
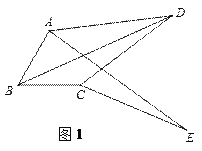
֤������ͼ2������AC����BA=BC���ҡ�ABC=60�� ���ABC�ǵȱ�������
���ACB=60�㣬��CA=CB�߽��߶�CD�Ƶ�C˳ʱ����ת60��õ��߶�CE ��CD=CE���ҡ�DCE=60��
���BCD=��ACE
���BCD�ա�ACE��SAS�� ��AE=BD

��2���жϣ� ![]()
��3���жϣ� ![]()
֤������ͼ3,����AC����BA=BC���ҡ�ABC=60��
���ABC�ǵȱ������Σ����ACB=60�㣬��CA=CB
���߶�CF�Ƶ�C˳ʱ����ת60��õ��߶�CE������EF��EA
��CE=CF���ҡ�FCE=60�㣬���CEF�ǵȱ�������
���CFE=60�㣬��FE=FC�����BCF=��ACE
���BCF�ա�ACE��SAS������AE=BF
�ߡ�AFC=150��, ��CFE=60�㣬���AFE=90��
��Rt��AEF�� �� ![]()
��![]() .
.



 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���н��ס���������Ʒ���۸������30%����ͬʱ����30Ԫ���ۣ��۳���������Ʒ��������Ϊ60Ԫ����ס���������Ʒ����֮��ΪԪ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x=2��һԪ���η���x2��2mx+4=0��һ���⣬��m��ֵΪ�� ��
A.2
B.0
C.0��2
D.0��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
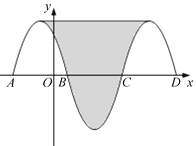
����Ŀ����ͼ��������y����x2��2x��3��x�ύ�ڵ�A��B������������x�ἰ���Ϸ��IJ��ּ���C1����C1���ڵ�B���ĶԳƵ�C2��C2��x�ύ����һ��C����C2���ڵ�C���ĶԳƵ�C3������C1��C3�Ķ��㣬��ͼ����Ӱ���ֵ����Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������ABCD��λ����ͼ��ʾ����A������Ϊ��1��0������D������Ϊ��0��2�����ӳ�CB��x���ڵ�A1 �� ��������A1 B1 C1 C���ӳ�C1B1��x���ڵ�A2 �� ��������A2B2C2C1���������Ĺ��ɽ�����ȥ����������ABCD���һ�������Σ����2010�������ε����Ϊ��������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ�����������Ȼ��Ҫ�������
����1+2+3+��+100=�����һ��һ��˳�������Ȼ̫�鷳��������ϸ������100��������Ȼ���Ĺ��ɺ��ص������Է������üӷ������������ǿ��Դ�������������ٶȵģ���Ϊ1+100=2+99=3+98=��=50+51=101�����Խ�������ʽ�и�������������������Ժ������Ժܿ���������
��1+2+3+4+5+��+100
=��1+100��+��2+99��+��3+98��+��+��50+51��
=101�� = ��
��1����ȫ������������
��2���������1+2+3+4+5+6+��+��2n��2��+��2n��1��+2n= ��
��3���Լ�����a+��a+b��+��a+2b��+��a+3b��+��+��a+99b����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���ABCO�������Σ���֪��C������Ϊ��![]() �� 1�������B������Ϊ��������
�� 1�������B��������������
A.��![]() ��1��
��1��![]() +1��
+1��
B.��![]() ��1��1��
��1��1��
C.��1��![]() +1��
+1��
D.��![]() ��1��2��
��1��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������8�֣�ij�ֵ��Ӳ�Ʒ��![]() ������������Ʒ�ʹ�Ʒ����֪��������ȡ��һ����ȡ�õIJ�ƷΪ��Ʒ�ĸ���Ϊ
������������Ʒ�ʹ�Ʒ����֪��������ȡ��һ����ȡ�õIJ�ƷΪ��Ʒ�ĸ���Ϊ![]() ��
��
��1��������Ʒ����Ʒ ����
��2�������������ȡ��![]() ���������б�����״ͼ��ȡ��
���������б�����״ͼ��ȡ��![]() ��������Ʒ�ĸ��ʣ�
��������Ʒ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ3��a2b��ab2����2��2a2b��1��+3ab2��1������a����2��b��1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com