
【题目】某市体育中考现场考试内容有三项:50米跑为必测项目.另在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项.
(1)每位考生有_________种选择方案;
(2)求小明与小刚选择同种方案的概率.
【答案】(1)4;(2)![]()
【解析】
(1)先列举出毎位考生可选择所有方案:50米跑、立定跳远、坐位体前屈(用A表示);50米跑、实心球、坐位体前屈(用B表示);50米跑、立定跳远、1分钟跳绳(用C表示);50米跑、实心球、1分钟跳绳(用D表示);共用4种选择方案.
(2)利用数形图展示所有16种等可能的结果,其中选择两种方案有12种,根据概率的概念计算即可.
解:(1)毎位考生可选择:50米跑、立定跳远、坐位体前屈(用A表示);50米跑、实心球、坐位体前屈(用B表示);50米跑、立定跳远、1分钟跳绳(用C表示);50米跑、实心球、1分钟跳绳(用D表示);共用4种选择方案.
故答案为:4.
(2)用![]() 、
、![]() 、
、![]() 、
、![]() 代表四种选择方案,用树状图分析如下:
代表四种选择方案,用树状图分析如下:
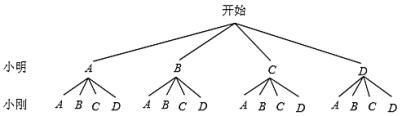
用列表法分析如下:
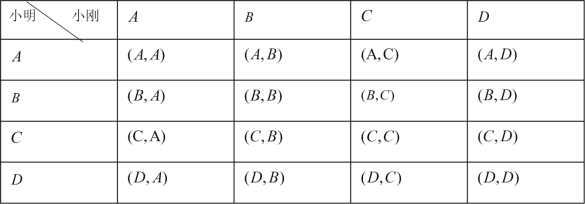
∴小明与小刚选择同种方案![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】密码锁有三个转轮,每个转轮上有十个数字:0,1,2,…9.小黄同学是9月份中旬出生,用生日“月份+日期”设置密码:9××(注:中旬为某月中的11日﹣20日),小张同学要破解其密码:
(1)第一个转轮设置的数字是9,第二个转轮设置的数字可能是 .
(2)请你帮小张同学列举出所有可能的密码,并求密码数能被3整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣1,0)和点B,且OB=3OA,与y轴交于点C,此抛物线顶点为点D.
(1)求抛物线的表达式及点D的坐标;
(2)如果点E是y轴上的一点(点E与点C不重合),当BE⊥DE时,求点E的坐标;
(3)如果点F是抛物线上的一点.且∠FBD=135°,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
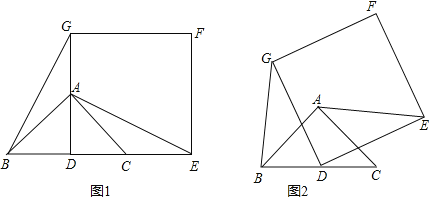
【题目】如图1,已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点D是BC的中点
,点D是BC的中点![]() 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
![]() 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______;
![]() 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转![]() ,
,
![]() 判断
判断![]() 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论;
![]() 若
若![]() ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com