
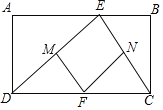
【题目】如图,四边形ABCD是矩形,点E是边AB上一个动点,点F,M,N分别是DC,DE,CE的中点.
(1)求证:△DMF≌△FNC;
(2)若四边形MFNE是正方形,求AD:AB的值.
【答案】(1)详见解析;(2)AD:AB=1:2.
【解析】
(1)由三角形中位线定理可得DM=EM=FN,MF=EN=CN,DF=CF,由“SSS”可证△DMF≌△FNC;
(2)由正方形的性质可得EN=NF=EM=MF,NE⊥EM,可得DE=EC,可得∠EDC=∠ECD=45°,可证AD=AE,BC=BE,即可求AD:AB的值.
证明:(1)∵点F,M,N分别是DC,DE,CE的中点.
∴DM=EM=FN,MF=EN=CN,DF=CF
∴△DMF≌△FNC(SSS)
(2)∵四边形MENF是正方形.
∴EN=NF=EM=MF,NE⊥EM,
∴DE=EC
∴∠EDC=∠ECD=45°,
∵AB∥CD
∴∠AED=∠EDC=45°,∠BEC=∠ECD=45°
∴∠A=∠B=90°
∴∠AED=∠ADE=45°,∠BEC=∠BCE=45°
∴AD=AE,BC=BE,
∴AB=AE+BE=2AD
∴AD:AB=1:2.


科目:初中数学 来源: 题型:
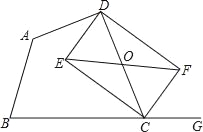
【题目】已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AD=5,AB=3.若M为射线AD上的一个动点,将△ABM沿BM折叠得到△NBM.若△NBC是直角三角形.则所有符合条件的M点所对应的AM长度的和为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
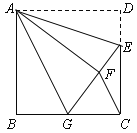
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,2016年底全球支付宝用户数为4.5亿,2018年底达到9亿假设每年增长率相同,则按此速度增长,估计2019年底全球支付宝用户可达(![]() ≈1.414)( )
≈1.414)( )
A.11.25亿B.13.35亿C.12.73亿D.14亿
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y4x4与x轴,y轴分别交于点A,B,点A在抛物线yax2bx3a(a0)上,将点B向右平移3个单位长度,得到点C.
(1)抛物线的顶点坐标为 (用含a的代数式表示)
(2)若a1,当t-1≤x≤t时,函数yax2bx3a(a0)的最大值为y1,最小值为y2,且y1y22,求t的值;
(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
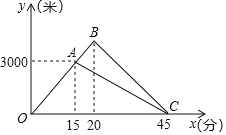
【题目】张琪和爸爸到曲江池遗址公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,张琪继续前行5分钟后也原路返回,两人恰好同时到家张琪和爸爸在整个运动过程中离家的路点y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示
(1)求爸爸返问时离家的路程y2(米)与运动时间x(分)之间的函数关系式;
(2)张琪开始返回时与爸爸相距多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运动品牌对第一季度A、B两款运动鞋的销售情况进行统计,两款运动鞋的销售量及总销售额如图所示:
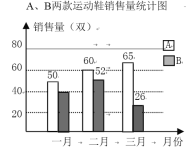
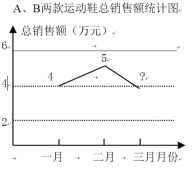
(1)一月份B款运动鞋的销售量是A款的80%,则一月份B款运动鞋销售了多少双?
(2)第一季度这两款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量)
(3)结合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com