
 如图,在一张长为5cm,宽为4cm的长方形纸片上,现要剪下一个腰长为3cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上),则剪下的等腰三角形的底边的长为3$\sqrt{2}$,2$\sqrt{6}$,$\sqrt{30}$cm.
如图,在一张长为5cm,宽为4cm的长方形纸片上,现要剪下一个腰长为3cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上),则剪下的等腰三角形的底边的长为3$\sqrt{2}$,2$\sqrt{6}$,$\sqrt{30}$cm. 分析 因为等腰三角形腰的位置不明确,所以分(1)腰长在矩形相邻的两边上,(2)一腰在矩形的宽上,(3)一腰在矩形的长上,三种情况讨论.(1)△AEF为等腰直角三角形,直接利用直接勾股定理求解即可;(2)先利用勾股定理求出AE边上的高BF,再利用勾股定理求出结论;(3)先利用勾股定理求出BF,再利用勾股定理求出底边.
解答 解:分三种情况计算:
(1)当AE=AF=3时,如图:
∴EF=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$;
(2)当AE=EF=3时,如图: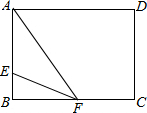
则BE=4-3=1,
BF=$\sqrt{E{F}^{2}-B{E}^{2}}$=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,
∴AF$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{{4}^{2}+(2\sqrt{2})^{2}}$=2$\sqrt{6}$;
(3)当AE=EF=3时,如图:
则DE=5-3=2,
DF=$\sqrt{E{F}^{2}-D{E}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
∴AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=$\sqrt{{5}^{2}+(\sqrt{5})^{2}}$=$\sqrt{30}$,
故答案为:$3\sqrt{2},2\sqrt{6},\sqrt{30}$.
点评 本题主要考查矩形的角是直角的性质和勾股定理的运用,要根据三角形的腰长的不确定分情况讨论,有一定的难度.


科目:初中数学 来源: 题型:选择题
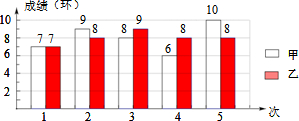
| A. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2=S_乙^2$ | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2>S_乙^2$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
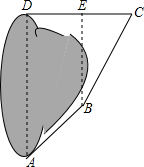 某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
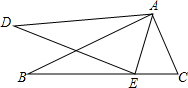 如图,在△ABC和△ADE中,点E在BC上,∠B=∠D,AB=AD,∠EAC=∠DAB
如图,在△ABC和△ADE中,点E在BC上,∠B=∠D,AB=AD,∠EAC=∠DAB查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com