
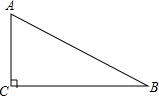
 如图,△ABC中,∠ACB=90°,tanA=$\frac{4}{3}$,AB=15,AC=9.
如图,△ABC中,∠ACB=90°,tanA=$\frac{4}{3}$,AB=15,AC=9. 分析 根据锐角三角函数的定义先设BC=4x,得出AC=3x,再根据勾股定理求出求出x的值,从而得出AC.
解答 解:∵∠ACB=90°,tanA=$\frac{BC}{AC}$=$\frac{4}{3}$,
∴设BC=4x,则AC=3x,
∵AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=15,
∴15=$\sqrt{(4x)^{2}+(3x)^{2}}$,
解得:x2=9,
∴x1=3或x2=-3(不合题意,舍去),
∴AC=3x=9;
故答案为:9.
点评 此题考查了解直角三角形,用到的知识点是锐角三角函数和勾股定理;求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )
如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )| A. | 25° | B. | 30° | C. | 40° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
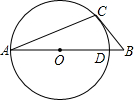 如图,AC是⊙O的弦,CB是⊙O的切线,C为切点,AB经过圆心与⊙O的交点为D,若∠B=50°,AD=10,则$\widehat{CD}$的长为$\frac{10}{9}$π.(结果保留π)
如图,AC是⊙O的弦,CB是⊙O的切线,C为切点,AB经过圆心与⊙O的交点为D,若∠B=50°,AD=10,则$\widehat{CD}$的长为$\frac{10}{9}$π.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
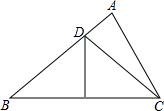 如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.
如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
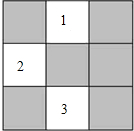 某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.
某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
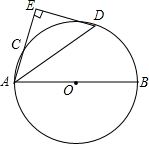 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com