
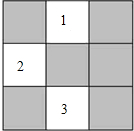
 某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.
某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.分析 (1)由共有9个方格,需保留区域小方格有6个,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与编号为1、2的两个小方格被粘贴的情况,再利用概率公式即可求得答案.
解答 解:(1)∵共有9个方格,需保留区域小方格有6个,
∴小明将这份通知粘贴在需保留区域小方格的概率为:$\frac{6}{9}$=$\frac{2}{3}$;
(2)画树状图得: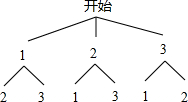
∵共有6种等可能的结果,编号为1、2的两个小方格被粘贴的有2种情况,
∴编号为1、2的两个小方格被粘贴的概率是:$\frac{2}{6}$=$\frac{1}{3}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:填空题
 如图,抛物线C1是二次函数y=x2-10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;它与x轴的另一交点为A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…,若某段抛物线上有一点
如图,抛物线C1是二次函数y=x2-10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;它与x轴的另一交点为A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…,若某段抛物线上有一点查看答案和解析>>
科目:初中数学 来源: 题型:填空题
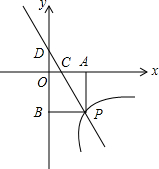 如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且
如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 己知常数a(a是常数)满足下面两个条件:
己知常数a(a是常数)满足下面两个条件:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
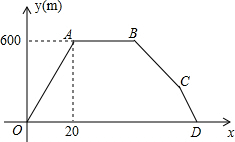 某山山脚的M处到山顶的N处有一条长为600米的登山路,小李沿此路从M走到N,停留后再原路返回,期间小李离开M处的路程y米与离开M处的时间x分(x>0)之间的函数关系如图中折线OABCD所示.
某山山脚的M处到山顶的N处有一条长为600米的登山路,小李沿此路从M走到N,停留后再原路返回,期间小李离开M处的路程y米与离开M处的时间x分(x>0)之间的函数关系如图中折线OABCD所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com