Question

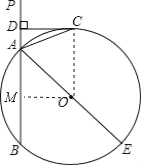
【题目】如图，已知直线PA交⊙O于A、B两点，CD是⊙O的切线，切点且C，过点C作CD⊥PA于D，若AD：DC=1：3，AB=8，求⊙O的半径．

Answer 1

【答案】5

【解析】试题分析：过O作OM⊥AB于M，得出矩形OMDC，推出OM=CD，OC=AM+AD，求出AM的长，设AD=x，则DC=OM=3x，OA=OC=DM=DA+AM=x+4，得出方程（x+4）2=42+（3x）2，求出x的值即可求出⊙O的半径．

试题解析：过O作OM⊥AB于M，连接OC，

即∠OMA=90°，

∵AB=8，

∴由垂径定理得：AM=4，

∵CD是切线，∴∠OCD=90°，

∵∠MDC=∠OMA=∠DCO=90°，

∴四边形DMOC是矩形，

∴OC=DM，OM=CD，

∵AD：DC=1：3，

∴设AD=x，则DC=OM=3x，OA=OC=DM=DA+AM=x+4，

∵在Rt△AMO中，∠AMO=90°，根据勾股定理得：AO2=42+OM2，

∴（x+4）2=42+（3x）2，

解得 x1=0（不合题意，舍去），x2=1，

则 OA=MD=x+4=5，

∴⊙O的半径是5．