
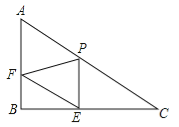
【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.
【答案】(1)![]() (0<x<20);(2)当x=10或x=16,存在点P使△PEF是Rt△.
(0<x<20);(2)当x=10或x=16,存在点P使△PEF是Rt△.
【解析】(1)在Rt△ABC中,∠B=90°,AC=20,AB=10,∴sinC=![]() ,∵PE⊥BC于点E,∴sinC=
,∵PE⊥BC于点E,∴sinC=![]() =
=![]() ,∵PC=x,PE=y,∴
,∵PC=x,PE=y,∴![]() (0<x<20);
(0<x<20);
(2)存在点P使△PEF是Rt△,①如图1,当∠FPE=90°时,四边形PEBF是矩形,BF=PE=![]() x,四边形APEF是平行四边形,PE=AF=
x,四边形APEF是平行四边形,PE=AF=![]() x,∵BF+AF=AB=10,∴x=10;
x,∵BF+AF=AB=10,∴x=10;
②如图2,当∠PFE=90°时,Rt△APF∽Rt△ABC,∠ARP=∠C=30°,AF=40﹣2x,平行四边形AFEP中,AF=PE,即:40﹣2x=![]() x,解得x=16;
x,解得x=16;
③当∠PEF=90°时,此时不存在符合条件的Rt△PEF.
综上所述,当x=10或x=16,存在点P使△PEF是Rt△.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】2015年5月6日,凉山州政府在邛海“空列”项目考察座谈会上与多方达成初步合作意向,决定共同出资60.8亿元,建设40千米的邛海空中列车.据测算,将有24千米的“空列”轨道架设在水上,其余架设在陆地上,并且每千米水上建设费用比陆地建设费用多0.2亿元.
(1)求每千米“空列”轨道的水上建设费用和陆地建设费用各需多少亿元?
(2)预计在某段“空列”轨道的建设中,每天至少需要运送沙石1600m3,施工方准备租用大、小两种运输车共10辆,已知每辆大车每天运送沙石200m3,每辆小车每天运送沙石120m3,大、小车每天每辆租车费用分别为1000元、700元,且要求每天租车的总费用不超过9300元,问施工方有几种租车方案?哪种租车方案费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班50名学生期末考试数学成绩(单位:分)的频率分布直方图如图所示,其中数据不在分点上,对图中提供的信息作出如下的判断: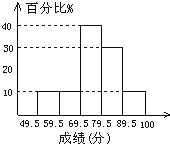
②成绩在79.5~89.5分段的人数占30%;
③成绩在79.5分以上的学生有20人;
④本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 互补的两个角是邻补角 B. 两直线平行,同旁内角相等
C. “同旁内角互补”不是命题 D. “相等的两个角是对顶角”是假命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人利用不同的交通工具,沿同一路线分别从A、B两地同时出发匀速前往C地(B在A、C两地的途中).设甲、乙两车距A地的路程分别为y甲、y乙(千米),行驶的时间为x(小时),y甲、y乙与x之间的函数图象如图所示.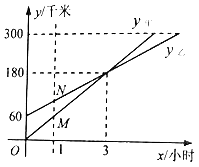
(1)直接写出y甲、y乙与x之间的函数表达式;
(2)如图,过点(1,0)作x轴的垂线,分别交y甲、y乙的图象于点M,N.求线段MN的长,并解释线段MN的实际意义;
(3)在乙行驶的过程中,当甲、乙两人距A地的路程差小于30千米时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出一种运算:对于函数y=xn,规定y′=nxn﹣1.例如:若函数y=x4,则有y′=4x3.已知函数y=x3,则方程y′=12的解是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com