
【题目】某班50名学生期末考试数学成绩(单位:分)的频率分布直方图如图所示,其中数据不在分点上,对图中提供的信息作出如下的判断: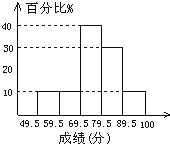
②成绩在79.5~89.5分段的人数占30%;
③成绩在79.5分以上的学生有20人;
④本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A.4个
B.3个
C.2个
D.1个
科目:初中数学 来源: 题型:
【题目】某市火车运货站现有甲种货物1530吨,乙种货物1150 吨,安排用一列货车将这批货物运往广州,这种货车可挂A、B两种不同规格的货厢50节.已知用一节A型货厢的运费是0.5万元,用一节B型货厢的运费是0.8万元.
(1)设运输这批货物的总运费y(万元),用A型货厢的节数为x(节),试写出y与x之间的函数关系式;
(2)已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢.按此要求安排A、B两种货厢的节数,有哪几种运输方案?请你设计出来;
(3)利用函数性质说明,在这些方案中,哪种方案总运费最少?最少运费是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明借到一本有72页的图书,要在10天之内读完,开始2天每天只读5页,那么以后几天里每天至少要读多少页?设以后几天里每天要读x页,所列不等式为( )
A. 10+8x≥72 B. 2+10x≥72
C. 10+8x≤72 D. 2+10x≤72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别是OB、OC的中点.
(1)求证:EN与DM互相平分;
(2)若AB=AC,判断四边形DEMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
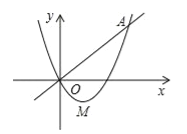
【题目】如图,在平面直角坐标系xOy中,一次函数y=x与二次函数![]() 的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
(1)求二次函数的表达式;
(2)长度为![]() 的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
(3)直线OA上是否存在点E,使得点E关于直线MA的对称点F满足S△AOF=S△AOM?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
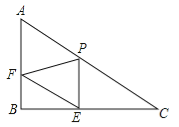
【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆一中渝北分校积极组织学生开展课外阅读活动,为了解全校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题: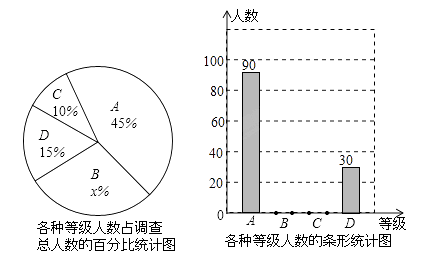
(1)求这次抽查的学生总数是多少人,并求出x的值;
(2)将不完整的条形统计图补充完整;
(3)若该校共有学生3600人,试估计每周课外阅读时间量满足2≤t<4的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com