
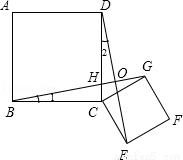
(11分)如图,四边形ABCD是正方形,以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE,猜想如图中线段BG、线段DE的关系并证明.

详见解析
【解析】
试题分析:由于四边形ABCD、四边形CEFG是正方形,那么又BC=CD,CG=CF,∠BCD=∠GCE=90°,利用等式性质有∠BCD+∠DCG=∠GCE+∠DCG,即∠BCG=∠DCE,利用SAS可证△BCG≌△DCE,那么有BG=DE,∠1=∠2,又∵∠BHC=∠DHO,于是可得∠1+∠BHC=∠2+∠DHO,即∠2+∠DHO=90°,结合三角形内角和定理可得∠DOH=90°,从而BG⊥DE.
试题解析:猜想:BG=DE,且BG⊥DE.
证明:如右图所示,
∵四边形ABCD、四边形CEFG是正方形,
∴∠BCD=∠GCE=90°,BC=CD,CE=CG,
∴∠BCD+∠DCG=∠GCF+∠DCG,
即∠BCG=∠DCE,
∴△BCG≌△DCE,
∴∠1=∠2,BG=DE,
又∵∠BHC=∠DHO,
∴∠1+∠BHC=∠2+∠DHO,
即∠2+∠DHO=90°,
∴∠DOH=180°﹣90°=90°,
∴BG⊥DE.
考点:1.正方形的性质;2.全等三角形的判定与性质.
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性

科目:初中数学 来源:2014-2015学年江苏省徐州市九年级上学期第一次质检数学试卷(解析版) 题型:填空题
在实数范围内定义一种运算规定a※b=a2-b2,则方程(x+2)※5=0的解为
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第一次摸底数学试卷(解析版) 题型:选择题
已知关于x的一元二次方程(a-1)x -2x+1=0有两个不相等的实数根,则a的取值范围是( )
-2x+1=0有两个不相等的实数根,则a的取值范围是( )
A.a<2 B.a>2 C.a<2且a≠1 D.a<-2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第一次摸底数学试卷(解析版) 题型:选择题
已知4个数据: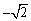 ,
,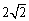 ,a,b,其中a,b是方程
,a,b,其中a,b是方程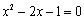 的两个根,则这4个数据的中位数是( )
的两个根,则这4个数据的中位数是( )
A.1 B.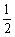 C.2 D.
C.2 D.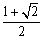
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省平顶山市九年级上学期第一次月考数学试卷(解析版) 题型:填空题
如图,已知菱形ABCD的两条对角线分别是6和8,M、N分别是BC、CD的中点,点P是对角线BD上一点,则PM+PN的最小值是________.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南平顶山四十三中八年级上学期第一次段测数学试卷(解析版) 题型:填空题
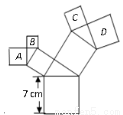
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和为___________cm2.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省人教版九年级下学期模拟数学试卷(解析版) 题型:解答题
某商店经营一批进价每件为2元的小商品,在市场营销的过程中发现:如果该商品按每件最低价3元销售,日销售量为18件,如果单价每提高1元,日销售量就减少2件.设销售单价为x(元),日销售量为y(件).
(1)写出日销售量y(件)与销售单价x(元)之间的函数关系式;
(2)设日销售的毛利润(毛利润=销售总额-总进价)为P(元),求出毛利润P(元)与销售单价x(元)之间的函数关系式;
(3)在下图所示的坐标系中画出P关于x的函数图象的草图,并标出顶点的坐标;

(4)观察图象,说出当销售单价为多少元时,日销售的毛利润最高?是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com