
����Ŀ����ͼ���ı���OMTN�У�OM=ON��TM=TN�����ǰ����������ڱ߷ֱ���ȵ��ı��ν������Σ�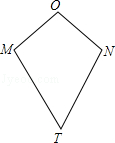
��1��̽�����ζԽ���֮���λ�ù�ϵ����֤����Ľ��ۣ�
��2��������ABCD�У���֪AB=AD=10��BC=CD��BC��AB��BD��ACΪ�Խ��ߣ�BD=16��
������ABC=90�㣬��AC�ij���
�ڹ���B��BF��CD��F��BF��AC�ڵ�E������DE�����ı���ABEDΪ����ʱ�����F��AB�ľ��룮
���𰸡�
��1��
�⣺��ͼ1������MN��OT���ڵ�A��
MN��OT�������ǣ�
��OM=ON��TM=TN��OT=OT��
���OMT�ա�ONT��
���MOT=��NOT��
��OM=ON��
��MN��OT
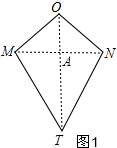
��2��
�⣺����ͼ2��ʾ��
���ı���ABCDΪ���Σ�
��AC��BD��
��AB=AD��
��OB=OD= ![]() BD=
BD= ![]() ��16=8��
��16=8��
�ɹ��ɶ����ã�AO= ![]() =6��
=6��
��OC=x��
�ߡ�ABC=90�㣬
��BC2=AC2��AB2��BC2=OC2+OB2��
��82+x2=��6+x��2��102��
��ã�x= ![]() ��
��
��AC=OA+OC=6+ ![]() =
= ![]() ��
��
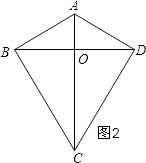
����ͼ3��ʾ��
���ı���ABEDΪ���Σ�
��BE=AD=10��EM=AM=6��
�ߡ�FBD=��FBD����BMC=��BFD=90�㣬
���BEM�ס�BDF��
�� ![]() ��
��
�� ![]() ��
��
��DF=9.6��
��Rt��DEF��EF= ![]() =2.8��
=2.8��
��BF=2.8+10=12.8��
�ߡ�BGF=��EFD=90�㣬��GBF=��FED��
���BGF�ס�EFD��
�� ![]() ��
��
��FG= ![]() =
= ![]() =12.288��
=12.288��
���F��AB�ľ���Ϊ12.288
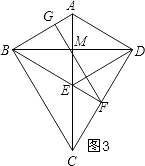
����������1����ͼ1��֤����OMT�ա�ONT���á�MOT=��NOT���ٸ��ݵ�����OMN���ߺ�һ�����ʵ�MN��OT����2������ͼ2���ȸ��ݹ��ɶ�����AO�ij��������ù��ɶ����з�����OC�ij�����AC=OC+AO������ó����ۣ�����ͼ3����֤����BEM�ס�BDF���ɵ� ![]() �����DF=9.6����ͨ�����ɶ�����EF�ij������BF�ij���ͨ��֤����BGF�ס�EFD����
�����DF=9.6����ͨ�����ɶ�����EF�ij������BF�ij���ͨ��֤����BGF�ס�EFD���� ![]() �����Կ�����FG�ij�������F��AB�ľ��룮
�����Կ�����FG�ij�������F��AB�ľ��룮
�����㾫����������Ĺؼ���������ɶ����ĸ�������֪ʶ������ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2���Լ������������ε��ж������ʵ����⣬�˽����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ӣ����ÿ3��һ�ѣ����÷��ꣻ���ÿ5��һ�ѣ����ʣ3�������ÿ7��һ�ѣ����Ҳʣ3����������ӵ�����������________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
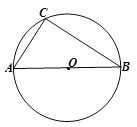
����Ŀ����֪����ͼ����֪��O����ABC�����Բ��ABΪ��O��ֱ����AC��6cm��BC��8cm.
(1)���O�İ뾶��
(2)���ó߹���ͼ������P��ʹ�õ�P���Ż�CAB��ʱ����PBC���������뱣����ͼ�ۼ����������PBC��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽ5(x��2)��8��6(x��1)��7����С������Ϊ����2x��ax��4�Ľ⣬��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и����ں���y��3x��2��ͼ���ϵ���( )
A. (1��1) B. (��1����1) C. (��1��1) D. (0��1)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������O�İ뾶Ϊ5cm����A��Բ��O�ľ���Ϊ6cm����ô��A���O��λ�ù�ϵ�� ( )
A. ��A��Բ��B. ��A��Բ��C. ��A��Բ��D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
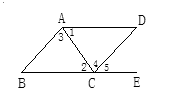
����Ŀ����ͼ���������ж� ![]() ��
�� ![]() ��������( )��.
��������( )��.
�� ![]() �� ��
�� �� ![]() ��
��
�� ![]() �� ��
�� �� ![]() .
.
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��a��b��ֱ��c���أ����1�͡�2��һ�ԣ� �� 
A.�Զ���
B.ͬλ��
C.�ڴ���
D.ͬ���ڽ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼa�dz�����ֽ������DEF=25�㣬��ֽ����EF�۵���ͼb������BF�۵���ͼc����ͼc�еġ�CFE�Ķ������㣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com