
【题目】从甲、乙两名射击选手中选出一名选手参加省级比赛,现对他们分别进行5次射击测试,成绩分别为(单位:环)甲:5、6、7、9、8;乙:8、4、8、6、9,
(1)甲运动员5次射击成绩的中位数为________环,极差是________环;乙运动员射击成绩的众数为________环.
(2)已知甲的5次成绩的方差为2,通过计算,判断甲、乙两名运动员谁的成绩更稳定.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
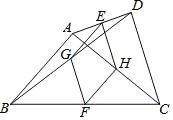
【题目】如图,在四边形ABCD中,AB=CD,E、F、G、H分别为AD、BC、BD、AC的中点,顺次连接E、G、F、H.
(1)猜想四边形EGFH是什么特殊的四边形,并说明理由;
(2)当∠ABC与∠DCB满足什么关系时,四边形EGFH为正方形,并说明理由;
(3)猜想:∠GFH、∠ABC、∠DCB三个角之间的关系.直接写出结果____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB=AD,BC=CD.
(1)如图1,请连接AC,BD,求证:AC垂直平分BD;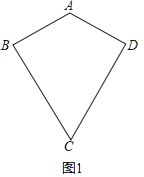
(2)如图2,若∠BCD=60°,∠ABC=90°,E,F分别为边BC,CD上的动点,且∠EAF=60°,AE,AF分别与BD交于G,H,求证:△AGH∽△AFE;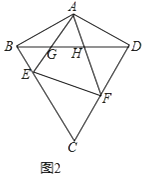
(3)如图3,在(2)的条件下,若 EF⊥CD,直接写出 ![]() 的值.
的值.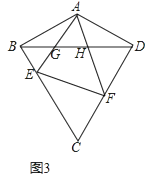
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2 , …,按图所示的方式放置.点A1、A2、A3 , …和点B1、B2、B3 , …分别在直线y=kx+b和x轴上.已知C1(1,﹣1),C2( ![]() ,
, ![]() ),则点A3的坐标是 .
),则点A3的坐标是 . 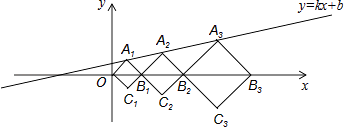
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=60°,OF⊥OE.
(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;
(2)求∠BOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,EF分别是 BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,且
,且![]() 满足方程组
满足方程组![]() ,连接
,连接![]() ,
,![]() .
.
(1)求![]() 的面积;
的面积;
(2)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 轴向左运动,连接
轴向左运动,连接![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() 秒,
秒, ![]() 的面积为
的面积为![]() , 试用含
, 试用含![]() 的式子表示
的式子表示![]() ;
;
(3)在![]() 的条件下,点
的条件下,点![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 在
在![]() 延长线上,且
延长线上,且![]() ,连接
,连接![]() , 当点
, 当点![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() ,
,![]() , 四边形
, 四边形![]() 的面积与
的面积与![]() 的面积比为
的面积比为![]() 时,求此时
时,求此时![]() 值和点
值和点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com