
【题目】在四边形ABCD中,AB=AD,BC=CD.
(1)如图1,请连接AC,BD,求证:AC垂直平分BD;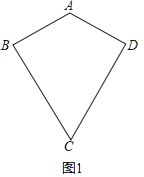
(2)如图2,若∠BCD=60°,∠ABC=90°,E,F分别为边BC,CD上的动点,且∠EAF=60°,AE,AF分别与BD交于G,H,求证:△AGH∽△AFE;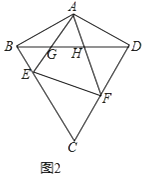
(3)如图3,在(2)的条件下,若 EF⊥CD,直接写出 ![]() 的值.
的值.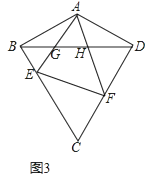
【答案】
(1)解:证明:如图1中,连接BD、AC.
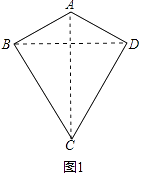
∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴AC是线段BD的垂直平分线,
即AC垂直平分线段BD.
(2)解:如图2中,将△ABE绕点A逆时针旋转120得到△ADM.连接AC交BD于O.
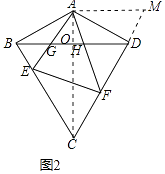
∵B、D关于AC对称,
∴∠ABC=∠ADC=90°,
∵∠BCD=60°,
∴∠BAD=120°,
∵∠EAF=60°,
∴∠BAE+∠DAF=∠DAF+∠DAM=60°,
∴∠FAE=∠FAM,
∵∠ADM=∠ABE=90°=∠ADF,
∴F、D、M共线,
∵FA=FA,AE=AM,
∴△FAE≌△FAM,
∴∠AFE=∠AFM,
∵∠CAD=∠CAB=60°=∠EAF,
∴∠GAO=∠DAF,
∵∠AGO+∠GAO=90°,∠AFD+∠FAD=90°,
∴∠AGO=∠ADF,
∴∠AGH=∠AFE,∵∠GAH=∠FAE,
∴△AGH∽△AFE.
(3)解:如图3中,连接AC交BD于O,作HM⊥AD于M.
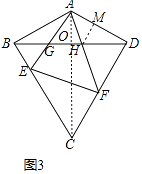
∵EF⊥CD,
∴∠EFD=90°,
由(2)可知∠AFD=∠AFE=∠AGO=45°,
∵∠ADF=90°,
∴AD=DF,设HM=AM=a,则DH=2a,DM= ![]() a,
a,
在Rt△ACD中,∵∠ACD=30°,AD=(1+ ![]() )a,
)a,
∴CD=BD= ![]() AD=(3+
AD=(3+ ![]() )a,
)a,
在Rt△AHD中,∵∠ADH=30°,AD=(1+ ![]() )a,
)a,
∴AO=OG= ![]() AD=
AD= ![]() a,OD=
a,OD= ![]() OA=
OA= ![]() a,
a,
∴OH=OD﹣DH= ![]() a﹣2a=
a﹣2a= ![]() a,
a,
∴GH=OG+OH= ![]() a,
a,
∴ ![]() =
= ![]() =
= ![]() .
.
【解析】(1)利用垂直平分线的判定定理及两点确定一条直线可证出;(2)通过旋转构造全等三角形,即△FAE≌△FAM,进而得出∠AFE=∠AFM,∠GAH=∠FAE,证出相似;(3)利用(2)的结论得出∠ADF=90°,AD=DF,设出参数HM=AM=a,运用三角函数定义,用a的代数式分别表示出BD,GH,可求出比值.
【考点精析】本题主要考查了相似三角形的判定与性质和锐角三角函数的定义的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能正确解答此题.


科目:初中数学 来源: 题型:
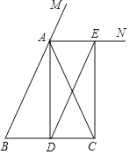
【题目】已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:我们把只有一组对角是直角的四边形叫做准矩形.
(1)图①、图②均为3×3的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.线段AB、BC的端点均在格点上,在图①、图②中各画一个准矩形ABCD,要求:准矩形ABCD的顶点D在格点上,且两个准矩形不全等.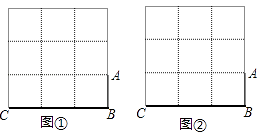
(2)如图③,正方形ABCD的边长为4,准矩形ABMN的顶点M、N分别在正方形ABCD的边上.若准矩形ABMN的一条对角线长为5,直接写出此时该准矩形的面积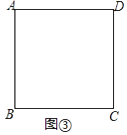
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y= ![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣ ![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )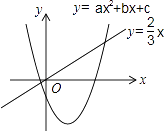
A.大于0
B.等于0
C.小于0
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表.
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,求工厂的最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过半径为6的圆O上一点A作圆O的切线l,P为圆O的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x的函数关系的是( )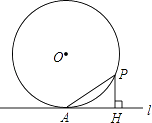
A.
B.
C.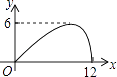
D.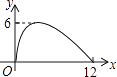
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名射击选手中选出一名选手参加省级比赛,现对他们分别进行5次射击测试,成绩分别为(单位:环)甲:5、6、7、9、8;乙:8、4、8、6、9,
(1)甲运动员5次射击成绩的中位数为________环,极差是________环;乙运动员射击成绩的众数为________环.
(2)已知甲的5次成绩的方差为2,通过计算,判断甲、乙两名运动员谁的成绩更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组 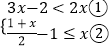 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得;
(Ⅱ)解不等式②,得;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为 . ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com