
【题目】某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表.
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,求工厂的最大利润?
【答案】
(1)解:设生产A种产品x件,则生产B种产品(10﹣x)件,于是有
x+3(10﹣x)=14,
解得:x=8,
则10﹣x=10﹣8=2(件)
所以应生产A种产品8件,B种产品2件;
(2)解:设总利润为y万元,应生产A种产品x件,则生产B种产品有(10﹣x)件,由题意有:
![]() ,
,
解得:2≤x<8;
利润y=x+3(10﹣x)=﹣2x+30,
则y随x的增大而减小,即可得,A产品生产越少,获利越大,
∴x=2时,可获得最大利润,其最大利润为2×1+8×3=26万元.
【解析】(1)由“计划获利14万元”可建立方程x+3(10﹣x)=14,得出结果;(2)由“资金不多于44万元,且获利多于14万元”建立不等式组,求出x的范围,建立关于利润的函数,利用函数的单调性求出最值.
【考点精析】解答此题的关键在于理解一元一次不等式组的应用的相关知识,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
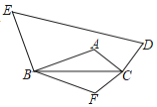
【题目】如图,在△ABC中,BC=10,BC边上的高为3.将点A绕点B逆时针旋转90°得到点E,绕点C顺时针旋转90°得到点D.沿BC翻折得到点F,从而得到一个凸五边形BFCDE,则五边形BFCDE的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,学校为了学生在班级将生活垃圾和废弃口罩分类丢弃,准备购买A,B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需270元,购买2个A型垃圾箱比购买3个B型垃圾箱少用80元.求每个A型垃圾箱和B型垃圾箱各多少元?学校购买A型垃圾桶8个,B型垃圾桶16个,共花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
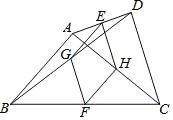
【题目】如图,在四边形ABCD中,AB=CD,E、F、G、H分别为AD、BC、BD、AC的中点,顺次连接E、G、F、H.
(1)猜想四边形EGFH是什么特殊的四边形,并说明理由;
(2)当∠ABC与∠DCB满足什么关系时,四边形EGFH为正方形,并说明理由;
(3)猜想:∠GFH、∠ABC、∠DCB三个角之间的关系.直接写出结果____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 . 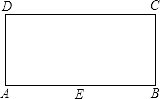
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB=AD,BC=CD.
(1)如图1,请连接AC,BD,求证:AC垂直平分BD;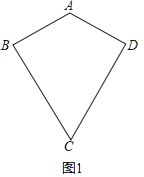
(2)如图2,若∠BCD=60°,∠ABC=90°,E,F分别为边BC,CD上的动点,且∠EAF=60°,AE,AF分别与BD交于G,H,求证:△AGH∽△AFE;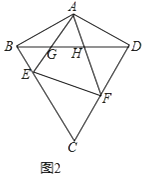
(3)如图3,在(2)的条件下,若 EF⊥CD,直接写出 ![]() 的值.
的值.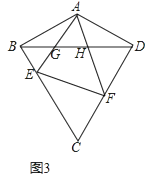
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2 , …,按图所示的方式放置.点A1、A2、A3 , …和点B1、B2、B3 , …分别在直线y=kx+b和x轴上.已知C1(1,﹣1),C2( ![]() ,
, ![]() ),则点A3的坐标是 .
),则点A3的坐标是 . 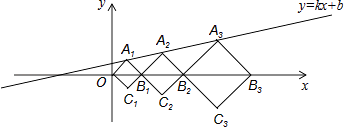
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,EF分别是 BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了进一步改进本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.

请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是 ;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com