
【题目】如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=60°,OF⊥OE.
(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;
(2)求∠BOE的度数.

【答案】(1)∠AOF=∠COF,理由详见解析;(2)∠BOE=120°.
【解析】
(1)求出∠AOD度数,求出∠AOE,求出∠AOF,即可得出答案;
(2)求出∠BOD度数,求出∠DOE度数,相加即可得出答案.
(1)答:∠AOF=∠COF,
证明:∵O是直线CD上一点,
∴∠AOC+∠AOD=180°,
∵∠AOC=60°,
∴∠AOD=180°﹣60°=120°,
∵OE平分∠AOD,
∴![]() .
.
∵OF⊥OE,
∴∠FOE=90°
∴∠AOF=∠FOE﹣∠AOE=90°﹣60°=30°,
∴∠COF=∠AOC﹣∠AOF=60°﹣30°=30°,
∴∠AOF=∠COF.
(2)解:∵∠AOC=60°,
∴∠BOD=∠AOC=60°,∠AOD=180°﹣60°=120°,
∵OE是∠AOD的平分线,
∴∠DOE=![]() ∠AOD=60°,
∠AOD=60°,
∴∠BOE=∠BOD+∠DOE=60°+60°=120°.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】完成下面的说理过程.
已知:如图,OA=OB,AC=BC.

试说明:∠AOC=∠BOC.
解:在△AOC和△BOC中,
因为OA=______,AC=______,OC=______,
所以________≌________(SSS),
所以∠AOC=∠BOC(__________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
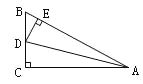
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+k(k为正整数)与坐标轴所构成的直角三角形的面积为Sk , 当k分别为1,2,3,…,199,200时,则S1+S2+S3+…+S199+S200=( )
A.10000
B.10050
C.10100
D.10150
查看答案和解析>>
科目:初中数学 来源: 题型:
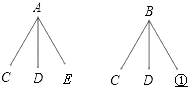
【题目】某电脑店有A、B两种型号的打印机和C、D、E三种芯片出售.每种型号的打印机均需要一种芯片配套才能打印.
(1)下列是该店用树形图或列表设计的配套方案,①的位置应填写 , ②的位置应 填写
(2)若仅有B型打印机与E种芯片不配套,则上面(1)中的方案配套成功率是
芯片 | C | D | E |
A | (A,C) | (A,D) | ② |
B | (B,C) | (B,D) | (B,E) |
查看答案和解析>>
科目:初中数学 来源: 题型:
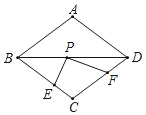
【题目】如图,在周长为12的菱形ABCD中,CE=1,CF=2,若点P为对角线BD上一动点,则PE+PF的最小值是( )
A. ![]() B. 2 C. 3 D. 5
B. 2 C. 3 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC. 
(1)求证:EF是⊙O的切线;
(2)求证:AC2=ADAB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一块破损的木板.
(1)请你设计一种方案,检验木板的两条直线边缘 AB、CD 是否平行;
(2)若 AB∥CD,连接 BC,过点 A 作 AM⊥BC 于 M,垂足为 M,画出图形,并写出∠BCD 与∠BAM 的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.

(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com