【题目】完成下面的说理过程．
已知：如图，OA＝OB，AC＝BC.
试说明：∠AOC＝∠BOC.
解：在△AOC和△BOC中，
因为OA＝______，AC＝______，OC＝______，
所以________≌________(SSS)，
所以∠AOC＝∠BOC(__________________)．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】如图，BA1和CA1分别是△ABC的内角平分线和外角平分线，BA2是∠A1BD的平分线，CA2是∠A1CD的平分线，BA3是∠A2BD的平分线，CA3是∠A2CD的平分线．若∠A1＝α，则∠A2019＝________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点O（0，0），A（0，1）是正方形OAA1B的两个顶点，以OA1对角线为边作正方形OA1A2B1 ， 再以正方形的对角线OA2作正方形OA1A2B1 ， …，依此规律，则点A2017的坐标是（ ）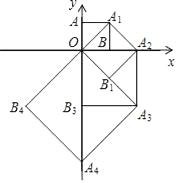
A.（0，21008）
B.（ 
， ）
C.（ 
，0）
D.（ ，- ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线 l1 经过点 A（5，0）和点 B（
，﹣5）
（1）求直线 l1 的表达式；
（2）设直线 l2 的解析式为 y=﹣2x+2，且 l2 与 x 轴交于点 D，直线 l1 交 l2 于点 C， 求△CAD 的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
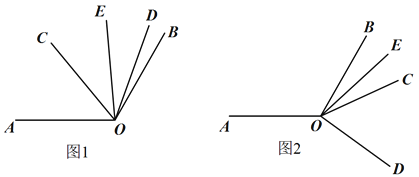
【题目】已知∠AOB=120°，∠COD=60°，OE平分∠BOC
（1）如图1．当∠COD在∠AOB的内部时
①若∠AOC=39°40′，求∠DOE的度数；
②若∠AOC=α，求∠DOE的度数（用含α的代数式表示），
（2）如图2，当∠COD在∠AOB的外部时，（1）中∠AOC与∠DOE的数量关系还成立吗？若成立，请推导出∠AOC与∠DOE的度数之间的关系；若不成立，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】以直线AB上一点O为端点作射线OC，使∠BOC＝60°，将一个直角三角形的直角顶点放在点O处．（注：∠DOE＝90°）
（1）如图1，若直角三角板DOE的一边OD放在射线OB上，则∠COE＝ °；
（2）如图2，将直角三角板DOE绕点O逆时针方向转动到某个位置，若OE恰好平分∠AOC，请说明OD所在射线是∠BOC的平分线；
（3）如图3，将三角板DOE绕点O逆时针转动到某个位置时，若恰好∠COD＝
∠AOE，求∠BOD的度数？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1)如图
示，AB∥CD，且点E在射线AB与CD之间，请说明∠AEC=∠A+∠C的理由．
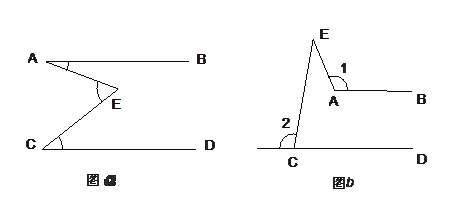
(2)现在如图b示，仍有AB∥CD，但点E在AB与CD的上方，①请尝试探索∠1,∠2,∠E三者的数量关系. ②请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB、CD相交于点O，OE是∠AOD的平分线，若∠AOC＝60°，OF⊥OE．
（1）判断OF把∠AOC所分成的两个角的大小关系并证明你的结论；
（2）求∠BOE的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
