
【题目】如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的平分线,CA2是∠A1CD的平分线,BA3是∠A2BD的平分线,CA3是∠A2CD的平分线.若∠A1=α,则∠A2019=________.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4-∠1=180°中能判断直线![]() ∥
∥![]() 的有( )
的有( )
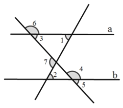
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= . 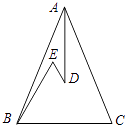
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的情景对话,然后解答问题: 
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
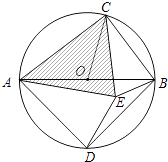
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆 ![]() 的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE. ①求证:△ACE是奇异三角形;
的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE. ①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 ![]() .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′. 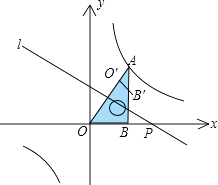
(1)当点O′与点A重合时,点P的坐标是;
(2)设P(t,0),当O′B′与双曲线有交点时,t的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班师生组织植树活动,上午8时从学校出发,到植树地点植树后原路返校,如图为师生离校路程s与时间t之间的图象.请回答下列问题: 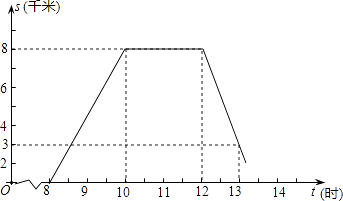
(1)求师生何时回到学校?
(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半小时到达植树地点,请在图中,画出该三轮车运送树苗时,离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
查看答案和解析>>
科目:初中数学 来源: 题型:
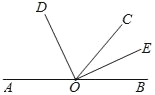
【题目】如图,点 A,O,B 在同一条直线上,OD,OE 分别平分∠AOC 和∠BOC.
(1)求∠DOE 的度数;
(2)如果∠COD=65°,求∠AOE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.
(1)请猜测OE与OF的大小关系,并说明你的理由;
(2)点O运动到何处时,四边形AECF是矩形?写出推理过程;
(3)点O运动到何处且△ABC满足什么条件时,四边形AECF是正方形?(写出结论即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的说理过程.
已知:如图,OA=OB,AC=BC.

试说明:∠AOC=∠BOC.
解:在△AOC和△BOC中,
因为OA=______,AC=______,OC=______,
所以________≌________(SSS),
所以∠AOC=∠BOC(__________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com