
【题目】阅读下面的情景对话,然后解答问题: 
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
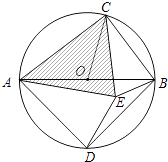
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆 ![]() 的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE. ①求证:△ACE是奇异三角形;
的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE. ①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
【答案】
(1)解:设等边三角形的一边为a,则a2+a2=2a2,
∴符合奇异三角形”的定义.
∴是真命题
(2)解:∵∠C=90°,
则a2+b2=c2①,
∵Rt△ABC是奇异三角形,且b>a,
∴a2+c2=2b2②,
由①②得:b= ![]() a,c=
a,c= ![]() a,
a,
∴a:b:c=1: ![]() :
: ![]()
(3)解:∵①AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ACB中,AC2+BC2=AB2,
在Rt△ADB中,AD2+BD2=AB2,
∵点D是半圆 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴AD=BD,
∴AB2=AD2+BD2=2AD2,
∴AC2+CB2=2AD2,
又∵CB=CE,AE=AD,
∴AC2+CE2=2AE2,
∴△ACE是奇异三角形;
②由①可得△ACE是奇异三角形,
∴AC2+CE2=2AE2,
当△ACE是直角三角形时,
由(2)得:AC:AE:CE=1: ![]() :
: ![]() 或AC:AE:CE=
或AC:AE:CE= ![]() :
: ![]() :1,
:1,
当AC:AE:CE=1: ![]() :
: ![]() 时,AC:CE=1:
时,AC:CE=1: ![]() ,即AC:CB=1:
,即AC:CB=1: ![]() ,
,
∵∠ACB=90°,
∴∠ABC=30°,
∴∠AOC=2∠ABC=60°;
当AC:AE:CE= ![]() :
: ![]() :1时,AC:CE=
:1时,AC:CE= ![]() :1,即AC:CB=
:1,即AC:CB= ![]() :1,
:1,
∵∠ACB=90°,
∴∠ABC=60°,
∴∠AOC=2∠ABC=120°.
∴∠AOC的度数为60°或120°.
【解析】(1)根据“奇异三角形”的定义与等边三角形的性质,求证即可;(2)根据勾股定理与奇异三角形的性质,可得a2+b2=c2与a2+c2=2b2 , 用a表示出b与c,即可求得答案;(3)①AB是⊙O的直径,即可求得∠ACB=∠ADB=90°,然后利用勾股定理与圆的性质即可证得;②利用(2)中的结论,分别从AC:AE:CE=1: ![]() :
: ![]() 与AC:AE:CE=
与AC:AE:CE= ![]() :
: ![]() :1去分析,即可求得结果.
:1去分析,即可求得结果.
【考点精析】掌握等边三角形的性质和勾股定理的概念是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
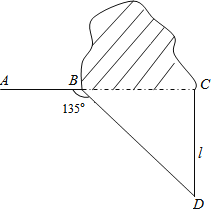
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
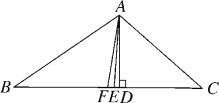
【题目】如图,AE是△ABC的角平分线,AD⊥BC于点D,点F为BC的中点,若∠BAC=104°,∠C=40°,则有下列结论:①∠BAE=52°;②∠DAE=2°;③EF=ED;④S△ABF=![]() S△ABC.其中正确的个数有( )
S△ABC.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①表示的是某综合商场今年1~5月的商品各月销售总额的情况,图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题: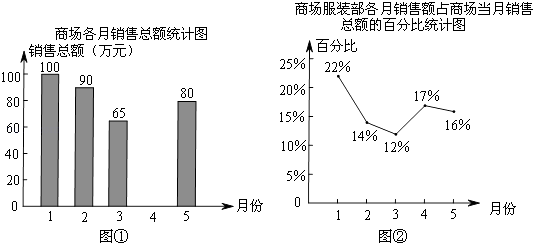
(1)来自商场财务部的数据报告表明,商场1~5月的商品销售总额一共是410万元,请你根据这一信息将图①中的统计图补充完整;
(2)商场服装部5月份的销售额是多少万元?
(3)小刚观察图②后认为,5月份商场服装部的销售额比4月份减少了.你同意他的看法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:(1)13=![]() ×12×22;(2)13+23=
×12×22;(2)13+23=![]() ×22×32;(3)13+23+33=
×22×32;(3)13+23+33=![]() ×32×42;(4)13+23+33+43=
×32×42;(4)13+23+33+43=![]() ×42×52;
×42×52;![]()
根据上述等式的规律,解答下列问题:
(1)写出第5个等式:_____;
(2)写出第n个等式(用含有n的代数式表示);
(3)设s是正整数且s≥2,应用你发现的规律,化简:![]() ×s2×(s+1)2﹣
×s2×(s+1)2﹣![]() ×(s﹣1)2×s2.
×(s﹣1)2×s2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,那么改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
1 | 2 | 3 | -7 |
-2 | -1 | 0 | 1 |
表1
(2)如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值.
a | a2-1 | -a | -a2 |
2-a | 1-a2 | a-2 | a2 |
表2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的平分线,CA2是∠A1CD的平分线,BA3是∠A2BD的平分线,CA3是∠A2CD的平分线.若∠A1=α,则∠A2019=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】妈妈要榨果汁,她有苹果、橙子、雪梨三种水果,且其颗数比为 9:7:6, 她榨完果汁后,苹果、橙子、雪梨的颗数比变为 6:3:4,已知妈妈榨果汁时没有使用雪梨, 小明根据他的发现利用所学的数学知识推断出妈妈榨果汁时只使用了橙子,妈妈告诉小明他的推断是完全正确的。请你尝试写出小明的推断过程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线 l1 经过点 A(5,0)和点 B(![]() ,﹣5)
,﹣5)
(1)求直线 l1 的表达式;
(2)设直线 l2 的解析式为 y=﹣2x+2,且 l2 与 x 轴交于点 D,直线 l1 交 l2 于点 C, 求△CAD 的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com