
【题目】设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,那么改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
1 | 2 | 3 | -7 |
-2 | -1 | 0 | 1 |
表1
(2)如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值.
a | a2-1 | -a | -a2 |
2-a | 1-a2 | a-2 | a2 |
表2
【答案】(1)见解析;(2)a=1.
【解析】
(1)根据某一行(或某一列)各数之和为负数,则改变改行(或该列)中所有数的符号,称为一次“操作”,先改变表1的第4列,再改变第2行即可;
(2)根据每一列所有数之和分别为2,0,-2,0,每一行所有数之和分别为-1,1,然后分别根据如果操作第三列或第一行,根据每行的各数之和与每列的各数之和均为非负整数,列出不等式组,求出不等式组的解集,即可得出答案.
(1)答案不唯一,如根据题意,得
1 | 2 | 3 | -7 |
-2 | -1 | 0 | 1 |
改变第四列的符号,得
1 | 2 | 3 | 7 |
-2 | -1 | 0 | -1 |
改变第二行的符号,得
1 | 2 | 3 | 7 |
2 | 1 | 0 | 1 |
(2)由表2,得每一列所有数之和分别为2,0,-2,0,每一行所有数之和分别为-1,1.则①如果操作第三列,得
a | a2-1 | a | -a2 |
2-a | 1-a2 | 2-a | a2 |
第一行之和为2a-1,第二行之和为5-2a,
![]() ,
,
解得:![]() ,
,
又∵a为整数,
∴a=1或a=2,
②如果操作第一行,得
-a | 1-a2 | a | a2 |
2-a | 1-a2 | a-2 | a2 |
那么每一列所有数之和分别为2-2a,2-2a2,2a-2,2a2.
由题意,得![]() ,
,
解得a=1.
此时2-2a2=0,2a2=2.
综上可知a=1.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】月球是地球的近邻,它的起源一直是人类不断探索的谜题之一.全球迄今进行了126次月球探测活动,因为研究月球可提高人类对宇宙的认识,包括认识太阳系的演化及特点,认识地球自然系统与太空自然现象之间的关系.我们已经认识到,在月球表面,白天阳光垂直照射的地方温度高达127℃,夜晚温度可降到﹣183℃.下面对“﹣183℃”的叙述不正确的是( )

A. ﹣183是一个负数
B. ﹣183表示在海平面以下183米
C. ﹣183在数轴上的位置在原点的左边
D. ﹣183是一个比﹣100小的数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上一点,且CE=CA,给出以下结论:①DE平分∠BDC; ②△BCE是等边三角形;③∠AEB=45°;④DE=AD+CD;正确的结论有_____.(请填序号)
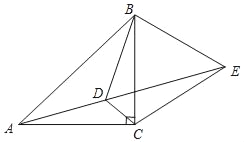
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°. 恒成立的结论有( )
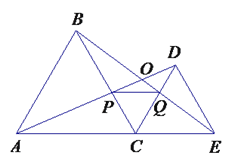
A. ①③④⑤ B. ①②④⑤
C. ①②③⑤ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的情景对话,然后解答问题: 
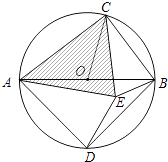
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆 ![]() 的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE. ①求证:△ACE是奇异三角形;
的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE. ①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班师生组织植树活动,上午8时从学校出发,到植树地点植树后原路返校,如图为师生离校路程s与时间t之间的图象.请回答下列问题: 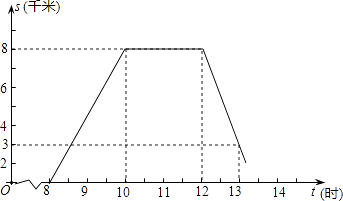
(1)求师生何时回到学校?
(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半小时到达植树地点,请在图中,画出该三轮车运送树苗时,离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
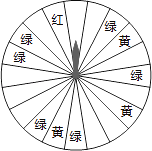
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com