
����Ŀ�������ǵ���Ľ��ڣ�������Դһֱ�������̽��������֮һ��ȫ�����������126������̽������Ϊ�о���������������������ʶ��������ʶ̫��ϵ���ݻ����ص㣬��ʶ������Ȼϵͳ��̫����Ȼ����֮��Ĺ�ϵ�������Ѿ���ʶ������������棬�������ⴹֱ����ĵط��¶ȸߴ�127�棬ҹ���¶ȿɽ�����183�森���������183��������������ȷ���ǣ�������

A. ��183��һ������
B. ��183��ʾ�ں�ƽ������183��
C. ��183�������ϵ�λ����ԭ������
D. ��183��һ���ȩ�100С����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й��Ŵ���ѧ���Ƕ��ڹ��ɶ����ķ��ֺ�֤������������ѧʷ�Ͼ��ж��صĹ��͵�λ����������ѧ�о��еļ̳кͷ�չ.����4��ȫ�ȵ�ֱ��������ƴ����ͼ��ʾ����ͼ��.Rt��ABC�У���ACB=90�㣬��![]() �������������ͼ�ν���������⣺
�������������ͼ�ν���������⣺
��1����˵��![]() ��
��
��2������������ε������10��С�����ε������2����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
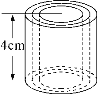
����Ŀ����ͼ��Բ���ĸ���4cm����Բ������뾶r(cm)�仯ʱ��Բ�������V(cm3)Ҳ��֮�仯��
(1)������仯�����У�д���Ա������������
(2) д��Բ�������V�����뾶r�Ĺ�ϵʽ��
(3)��Բ���ĵ���뾶��2cm�仯��8cmʱ��Բ��������ɶ���cm3�仯������cm3.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB�ߵĴ�ֱƽ����l1��BC�ڵ�D��AC�ߵĴ�ֱƽ����l2��BC�ڵ�E��l1��l2�ཻ�ڵ�O������OA��OB��OC.
(1)����ADE���ܳ�Ϊ6 cm����OBC���ܳ�Ϊ16 cm.
�����߶�BC�ij���
�����߶�OA�ij���
(2)����BAC��120�������DAE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
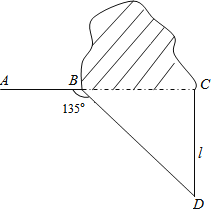
����Ŀ����ͼ����·����һ��ɽ������Ҫ��һ��������Ϊ�˼ӿ�ʩ�����ȣ�����Сɽ����һ��ͬʱʩ����Ϊ��ʹɽ����һ��Ŀ��ڵ�C��AB���ӳ����ϣ������C����ֱ��AB�Ĵ���L������B��һֱ�ߣ���ɽ���Ա߾���������L�ཻ��D�㣬��������ABD=135�㣬BD=800�ף���ֱ��L�Ͼ���D���Զ��C�����ڣ���![]() ��1.414����ȷ��1�ף�
��1.414����ȷ��1�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ�һֻ���ϴ�ԭ�������������������4����λ���ȵ����A��������������2����λ���ȵ����B��Ȼ��������������10����λ���ȵ����C��
��1���������������������ϱ�ʾ��A��B��C���㣻
��2�����ݵ�C�������ϵ�λ�ã���C���Կ��������ϴ�ԭ����������ĸ����������˼�����λ���ȵõ��ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
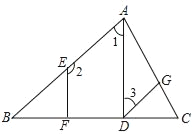
����Ŀ����ͼ����֪AD��BC��EF��BC������ֱ�ΪD��F����2+��3��180������˵������GDC����B���벹��˵�����̣�����������������Ӧ�����ɣ�
�⣺��AD��BC��EF��BC����֪��
���ADB����EFB��90���� ����
��EF��AD���� ������
���� ��+��2��180������ ������
�֡ߡ�2+��3��180������֪����
���1����3���� ������
��AB���� ������ ������
���GDC����B���� ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����û�������ij�ֻ��磬�������鷢��ÿ���ӯ����ÿ�����������һ���Ĺ�ϵ��ÿ��ֲ��3��ʱ��ƽ������ӯ��3Ԫ����ͬ����������������ÿ������1�꣬ƽ������ӯ���ͼ���0.5Ԫ��Ҫʹÿ���ӯ���ﵽ10Ԫ��ÿ��Ӧ��ֲ�����ꣿ С���Ľⷨ���£�
�⣺��ÿ�軨������x�꣬��ÿ�軨���У�x+3���꣬ƽ������ӯ��Ϊ��3��0.5x��Ԫ��
������ã�x+3����3��0.5x��=10��
���������ã�x2��3x+2=0
��������̣��ã�x1=1��x2=2��
��Ҫʹÿ���ӯ���ﵽ10Ԫ��ÿ��Ӧ��ֲ��4���5�꣮
��1�������漰����Ҫ������ÿ�軨��������ƽ������ӯ����ÿ�軨���ӯ���ȣ���д��������ͬ�ĵ�����ϵ�� ��
��2������һ����С������ͬ�ķ�������������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A����2��4��������ɵ�2��4�е����������ijһ��(��ijһ��)����֮��Ϊ��������ô�ı����(�����)���������ķ��ţ���Ϊһ������������
(1)���1��ʾ�����������������������ʹ�õ�������ÿ�еĸ���֮����ÿ�еĸ���֮�;�Ϊ�Ǹ���������д��ÿ���������������õ�������(д��һ�ַ�������)
1 | 2 | 3 | ��7 |
��2 | ��1 | 0 | 1 |
��1
(2)���2��ʾ������������һ�����������Ժ��ʹ�õ�������ÿ�еĸ���֮����ÿ�еĸ���֮�;�Ϊ�Ǹ�������������a��ֵ��
a | a2��1 | ��a | ��a2 |
2��a | 1��a2 | a��2 | a2 |
��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com