
【题目】(1)如图![]() 示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
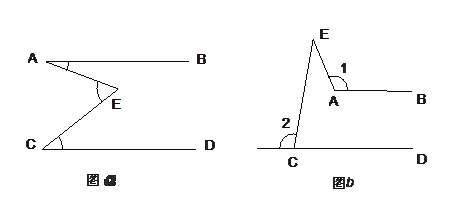
(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系. ②请说明理由.
【答案】(1)证明见解析(2)∠1+∠2-∠E=180°
【解析】
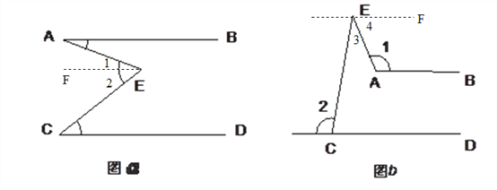
试题(1)过点E作EF∥AB,由两直线平行,内错角相等,得到∠A=∠1.
由平行的传递性得到EF // CD,再由平行线的性质得到∠2=∠C,由角的和差即可得到结论;
(2)过点E作EF∥AB,类似可得到结论.
试题解析:解:(1)过点E作EF∥AB,∴∠A=∠1(两直线平行,内错角相等).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠2=∠C(两直线平行,内错角相等).
∵∠AEC=∠1+∠2(图上可知),∴∠AEC=∠A+∠C(等量代换) ;
(2)∠1+∠2-∠E=180°.理由如下:
过点E作EF∥AB,∴∠4+∠1=180°(两直线平行,同旁内角互补).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠FEC=∠2(两直线平行,内错角相等),即∠3+∠4=∠2,∴∠4=∠2-∠3(等式性质),∴∠2-∠3+∠1=180°(等量代换),
即∠1+∠2-∠AEC=180°.


科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.
(1)请猜测OE与OF的大小关系,并说明你的理由;
(2)点O运动到何处时,四边形AECF是矩形?写出推理过程;
(3)点O运动到何处且△ABC满足什么条件时,四边形AECF是正方形?(写出结论即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的说理过程.
已知:如图,OA=OB,AC=BC.

试说明:∠AOC=∠BOC.
解:在△AOC和△BOC中,
因为OA=______,AC=______,OC=______,
所以________≌________(SSS),
所以∠AOC=∠BOC(__________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
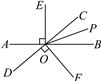
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,EO⊥AB于点O,FO⊥CD于点O.
(1)图中除直角外,还有其他相等的角,请写出两对:①______________;②______________.
(2)如果∠AOD=40°,那么:
①根据__________,可得∠BOC=________;
②求∠POF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?
(2)某蔬菜公司的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元,当地一家公司收购这种蔬菜140吨,该公司的加工生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天将这批蔬菜全部销售或加工完毕,为此公司研制了三种可行方案:
方案一:将蔬菜全部进行粗加工.
方案二:尽可能多地对蔬菜进行精加工,没来得及进行加工的蔬菜,在市场上直接销售.
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB.其中正确的有( )
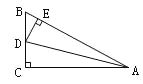
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+k(k为正整数)与坐标轴所构成的直角三角形的面积为Sk , 当k分别为1,2,3,…,199,200时,则S1+S2+S3+…+S199+S200=( )
A.10000
B.10050
C.10100
D.10150
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一块破损的木板.
(1)请你设计一种方案,检验木板的两条直线边缘 AB、CD 是否平行;
(2)若 AB∥CD,连接 BC,过点 A 作 AM⊥BC 于 M,垂足为 M,画出图形,并写出∠BCD 与∠BAM 的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com