
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,且
,且![]() 满足方程组
满足方程组![]() ,连接
,连接![]() ,
,![]() .
.
(1)求![]() 的面积;
的面积;
(2)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 轴向左运动,连接
轴向左运动,连接![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() 秒,
秒, ![]() 的面积为
的面积为![]() , 试用含
, 试用含![]() 的式子表示
的式子表示![]() ;
;
(3)在![]() 的条件下,点
的条件下,点![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 在
在![]() 延长线上,且
延长线上,且![]() ,连接
,连接![]() , 当点
, 当点![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() ,
,![]() , 四边形
, 四边形![]() 的面积与
的面积与![]() 的面积比为
的面积比为![]() 时,求此时
时,求此时![]() 值和点
值和点![]() 的坐标.
的坐标.

【答案】(1)6;(2)![]() ;(3)此时t的值为
;(3)此时t的值为![]() ,点E的坐标为(3,
,点E的坐标为(3,![]() ).
).
【解析】
(1)利用加减消元法解方程组即可求解;
(2)分类讨论:当点P在点O右侧时,当点P在点O左侧时,利用三角形的面积公式表示即可;
(3)根据题意画出相应的示意图,在x轴上取点F,使得MF=MB,连接FE、FN,在x轴的正半轴上取一点P ',使得OP'=OP,连接AP',过点N作NH⊥AB于点H,先证△P'AB≌△EFB,可得BE=8-2t,再证△NHB≌△AOP可得NH=AO=3,进而可表示出四边形![]() 的面积与
的面积与![]() 的面积,最后根据面积之比为49:10列出方程求解即可求得t的值,再过点E作EG⊥x轴于点G,进而可证得△EGB∽△AOB,通过相似三角形的性质即可求得点E的坐标.
的面积,最后根据面积之比为49:10列出方程求解即可求得t的值,再过点E作EG⊥x轴于点G,进而可证得△EGB∽△AOB,通过相似三角形的性质即可求得点E的坐标.
解:(1)![]()
①×3+②×2,得
13a=39,
a=3,
将a=3代入②得
b=4,
∴原方程组的解为![]()
∴A(0,3),B(4,0),
∴OA=3,OB=4,
∴![]()
答:![]() 的面积为6;
的面积为6;
(2)当0<t≤2时,
![]() ,
,
当t>2时,
![]() ,
,
综上所述:![]()
(3)如图,在x轴上取点F,使得MF=MB,连接FE、FN,在x轴的正半轴上取一点P ',使得OP'=OP,连接AP',过点N作NH⊥AB于点H,
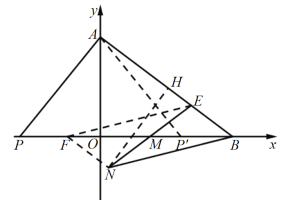
∵MF=MB,ME=MN,
∴四边形EFNB为平行四边形,
∴EF∥BN,
∴∠EFB=∠FBN,
∵OP'=OP,OA⊥x轴,
∴AP'=AP,
∴∠APO=∠AP'O,
∵∠APO=∠ABN,
∴∠AP'O=∠ABN,
∴∠P'AB+∠ABP'=∠FBN+∠ABP',
∴∠P'AB=∠FBN,
∴∠EFB=∠P'AB,
∵点M(1.5,0),点B(4,0)
∴MF=MB=2.5,
∴BF=5,
∵AB=5,
∴AB=BF,
在△P'AB与△EFB中,
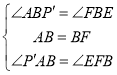
∴△P'AB≌△EFB(ASA)
∴BE=BP',
∵BP=2t,BO=4,
∴OP'=OP=2t-4,
∴BE=BP'=OB-OP'=4-(2t-4)=8-2t,
∵NH⊥AB,∠AOP=90°,
∴∠NHB=∠AOP=90°,
在△NHB与△AOP中,
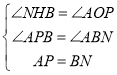
∴△NHB≌△AOP(AAS)
∴NH=AO=3,
∴![]()
![]()
![]()
∵ME=MN,
∴![]()
![]() ,
,
∵![]()
![]()
![]()
∴![]()
![]()
![]()
∵![]()
∴ ![]() ,
,
解得![]()
则BE=8-2t=![]()
如图,过点E作EG⊥x轴于点G,
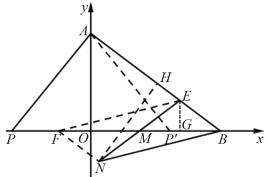
则EG∥y轴,
∴△EGB∽△AOB,
∴![]()
∴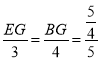
解得![]() ,
,![]() ,
,
∴![]()
∴点E的坐标为(3,![]() )
)
答:此时t的值为![]() ,点E的坐标为(3,
,点E的坐标为(3,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】新定义:我们把只有一组对角是直角的四边形叫做准矩形.
(1)图①、图②均为3×3的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.线段AB、BC的端点均在格点上,在图①、图②中各画一个准矩形ABCD,要求:准矩形ABCD的顶点D在格点上,且两个准矩形不全等.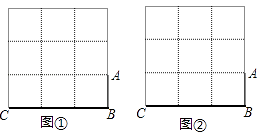
(2)如图③,正方形ABCD的边长为4,准矩形ABMN的顶点M、N分别在正方形ABCD的边上.若准矩形ABMN的一条对角线长为5,直接写出此时该准矩形的面积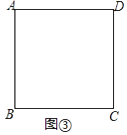
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名射击选手中选出一名选手参加省级比赛,现对他们分别进行5次射击测试,成绩分别为(单位:环)甲:5、6、7、9、8;乙:8、4、8、6、9,
(1)甲运动员5次射击成绩的中位数为________环,极差是________环;乙运动员射击成绩的众数为________环.
(2)已知甲的5次成绩的方差为2,通过计算,判断甲、乙两名运动员谁的成绩更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组 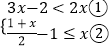 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得;
(Ⅱ)解不等式②,得;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为 . ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C,D两点间的距离.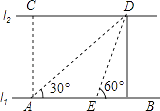
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两个等边△ABC和△DEF(DE>AB)如图所示摆放,点D是BC上的一点(除B、C点外).把△DEF绕顶点D顺时针旋转一定的角度,使得边DE、DF与△ABC的边(除BC边外)分别相交于点M、N.
(1)∠BMD和∠CDN相等吗?
(2)画出使∠BMD和∠CDN相等的所有情况的图形.
(3)在(2)题中任选一种图形说明∠BMD和∠CDN相等的理由.
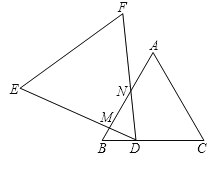
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2﹣2mx﹣3m2(m>0)与x轴交于A、B两点,A点在B点左边,与y轴交于C点,顶点为M.
(1)当m=1时,求点A、B、M坐标;
(2)如图(1)的条件下,若P为抛物线上一个动点,以AP为斜边的等腰直角的直角顶点Q在对称轴上,(A、P、Q按顺时针方向排列),求P点坐标.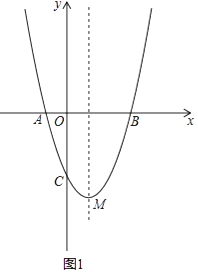
(3)如图2,若一次函数y=kx+b过B点且与抛物线只有一个公共点,平移直线y=kx+b,使其过抛物线的顶点M,与抛物线另一个交点为D,与x轴交于F点,当m变化时,求证:DF:MF是定值.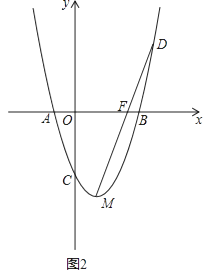
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com