
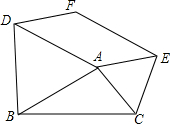
 如图,分别以△ABC的边AB、AC为边向形外作正△ABD和正△ACE,且DF∥AE,EF∥AD.
如图,分别以△ABC的边AB、AC为边向形外作正△ABD和正△ACE,且DF∥AE,EF∥AD.分析 (1)当∠BAC=150°时,可求得∠DAE=90°,四边形ADFE是矩形;
(2)当∠BAC=60°时,可求得∠DAE=180°,即D,A,E共线,则可得当∠BAC=60°时,平行四边形ADFE不存在;
(3)由四边形ADFE是平行四边形,可得AD=AE时,即AB=AC时,平行四边形ADFE是菱形;
(4)由四边形ADFE是平行四边形,可得AD=AE时,即AB=AC时,且满足∠BAC=150°,四边形ADFE是正方形.
解答 解:∵DF∥AE,EF∥AD,
∴四边形ADFE是平行四边形,
∵△ABD与△ACE是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°,
(1)当∠BAC=150°时,
理由:∵∠DAE=360°-∠BAC-∠DAB-∠EAC=90°,
∴∠BAC=150°,四边形ADFE为矩形.
(2)当∠BAC=60°时,平行四边形ADFE不存在.
理由:∵∠DAE=∠DAB+∠BAC+∠EAC=60°+60°+60°=180°,
∴D,A,E共线,
∴平行四边形ADFE不存在.
(3)当AB=AC时,平行四边形ADFE是菱形.
理由:∵AD=AB,AE=AC,AB=AC,
∴AD=AE,
∵四边形ADFE是平行四边形,
∴平行四边形ADFE是菱形.
(3)AB=AC时,且∠BAC=150°,四边形ADFE为正方形.
理由:∵AD=AB,AE=AC,AB=AC,
∴AD=AE,
∵四边形ADFE是平行四边形,
∴平行四边形ADFE是菱形.
∵∠BAC=150°,
∴∠DAE=90°,
∴四边形ADFE为正方形.
点评 此题考查了平行四边形的判定与性质,矩形、正方形、菱形的判定以及等边三角形的性质,注意掌握数形结合思想的应用.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题
 如图,∠ABM为直角,点C为线段BA的中点,点D为射线BM上的一个动点(不与点B重合),连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于点F.
如图,∠ABM为直角,点C为线段BA的中点,点D为射线BM上的一个动点(不与点B重合),连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
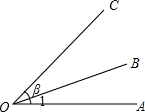 如图,下列表示角的说法,错误的是( )
如图,下列表示角的说法,错误的是( )| A. | ∠AOC也可用∠O表示 | B. | ∠1与∠AOB表示同一个角 | ||
| C. | ∠β表示的是∠BOC | D. | ∠AOB和∠BOC都不能用∠O表示 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
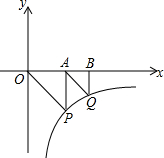 如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )
如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )| A. | (6,0) | B. | (9,0) | C. | ($\frac{3+3\sqrt{5}}{2}$,0) | D. | ($\frac{3\sqrt{2}+3}{2}$,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
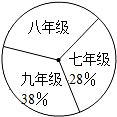 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )| 图书种类 | 频数 | 频率 |
| 科普知识 | 840 | B |
| 名人传记 | 816 | 0.34 |
| 漫画丛书 | A | 0.25 |
| 其它 | 144 | 0.06 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将正整数按如图所示的规律排列下去.若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示实数9,则192表示的有序实数对是(20,2).
将正整数按如图所示的规律排列下去.若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示实数9,则192表示的有序实数对是(20,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com