【题目】已知：如图，∠B=90°AB∥DF，AB=3cm，BD=8cm，点C是线段BD上一动点，点E是直线DF上一动点，且始终保持AC⊥CE。

（1）试说明：∠ACB =∠CED

（2）当C为BD的中点时， ABC与EDC全等吗？若全等，请说明理由；若不全等，请改变BD的长（直接写出答案），使它们全等。

（3）若AC=CE ,试求DE的长

（4）在线段BD的延长线上，是否存在点C，使得AC=CE，若存在，请求出DE的长及△AEC的面积；若不存在，请说明理由。

参考答案：

【答案】（1）见解析；（2）当C为BD中点时， ABC与 EDC不全等；（3）5cm；（4）见解析.

【解析】试题分析：（1）根据平行线的性质和三角形的内角和定理求出即可；
（2）根据全等三角形的判定定理进行判断，即可得出答案；
（3）根据全等得出对应边相等，即可得出答案；
（4）求出两三角形全等，得出对应边相等，再根据勾股定理和三角形面积公式求出即可．

试题解析：(1)

∵AC⊥CE，

(2)当C为BD的中点时，△ABC与△EDC不全等，当BD的长是6时，它们全等，

理由是：∵BD=6，C为BD中点，

∴BC=CD=3=AB，

在△ABC和△CDE中

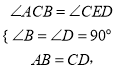
(3)∵在△ABC和△CDE中

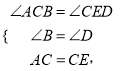
∴AB=CD=3cm，

∴DE=BC=8cm3cm=5cm；

(4)

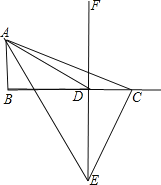
∵AC⊥CE，

∴∠ECD=∠BAC；

当CD=AB=3cm时，AC=CE，

∵在△ABC和△CDE中

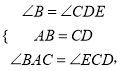
∴AC=CE，DE=BC=8cm，

∵AB=3cm，BC=BD+CD=8cm+3cm=11cm，

∴在中,由勾股定理得;

∴△AEC的面积是

关闭