
������10�֣���ͼ��������ABCD��������AEFG�й����Ķ���A����BG��DE��MΪDE���е㣬��AM.

��1����ͼ1��AE��AG�ֱ���AB��AD�غ�ʱ��AM��BG�Ĵ�С��λ�ù�ϵ�ֱ��� ��_ ____��
��2����ͼ1�е�������AEFG��A����ת����ͼ2����1���еĽ����Ƿ��Գ�������֤����Ľ��ۣ�
��3������ͼ1�е�������AEFG��A����ʱ����ת��������ABCD��ʱ����AM��BG�Ĵ�С��λ�ù�ϵ�ֱ���__________��____________��������ͼ3�л���ͼ�Σ���ֱ��д�����ۣ���Ҫ��֤��.
��1��BG=2AM��AM��BG��
��2��������֤����������
��3����ͼ��ʾ��BG=2AM��AM��BG����ͼ��������
��������
�����������1����֤����ABG�ա�ADE��BG=DE����AM�ǡ�ADE��б�������ߣ�����AM=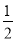 DE����AM=
DE����AM= 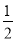 BG������BG=2AM���ɽ���ȼ������ϵ���ɵ�AM��BG��
BG������BG=2AM���ɽ���ȼ������ϵ���ɵ�AM��BG��
��2��Ҫ֤��BG=2AM���ɽ��߶�AM�ӳ�һ������ʱ���߶ξ͵���BG������ת��֤��������ȫ�ȣ��ó����ۣ�
��3��ѧ�����ǰ���ͼ�λ�ͼ��
�����������1��BG=2AM��AM��BG��
��2���ӳ�AM��K��ʹMK=AM������DK��EK����ƽ���ı���ADKE��
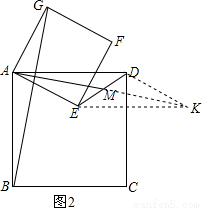
��EK��DC����EKD=��EAD��
���KDC=��GAD��
���BAG=��ADK��
��֤��ABG�ա�DAK��
��BG=2AM����DAK=��ABG��
��AM��BG��
��3����ͼ��ʾ��BG=2AM��AM��BG��
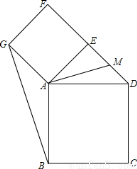
���㣺1����ת��������2��ȫ�������ε��ж���������3�������ε�������
��������� ����1���ı��� �ı��Σ��ı��εij�����ѧ�п��е��ص�����֮һ����ֵһ��Ϊ10-14�֣�������ѡ����գ����֤�����ں����ۺ���Ŀ��Ϊ��������Ϊ�С���Ҫ�������ݣ��ٶ���ε��ڽǺͣ���Ǻ͵������ͼ�ε���Ƕ�����ƽ���ı��Σ����Σ����Σ������Σ��������ε����ʺ��ж���ͻ�Ʒ����������ն���Σ��ı��ε����ʺ��ж���������Ǹ��ʽ����ע�������ı��ε����ʽ����й��ı��ε�֤������ע�������Ŀ�Ľ�𣬶������������ ��������

 �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���е�ͽ�����꼶10�µ�����ѧ�Ծ��������棩 ���ͣ������
ʵ�� �ǹ���
�ǹ���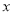 �ķ���
�ķ���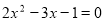 ��һ��������ʽ
��һ��������ʽ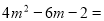
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�ڵ�һ���ʼ���ѧ�Ծ��������棩 ���ͣ������
д��һ��������ϵ��Ϊ1������һ������-2��һԪ���η���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�ڵ�һ���ʼ���ѧ�Ծ��������棩 ���ͣ�ѡ����
���䷽���ⷽ��x2-4x+1=0ʱ���䷽�����õķ����ǣ� ��
A����x-2��2=1 B����x-2��2=-1
C����x-2��2=3 D����x+2��2=3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�����ʡ�人��У���꼶9��������ѧ�Ծ��������棩 ���ͣ������
������6�֣���x1��x2�Ƿ���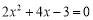 ������ʵ���������ⷽ�̣������д���ʽ��ֵ.[xx|k.Co
������ʵ���������ⷽ�̣������д���ʽ��ֵ.[xx|k.Co
��1����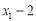 ����
���� ��
��
��2��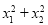
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ӱ�ʡɳ���о��꼶��ѧ�ڵ�һ��������ѧ�Ծ��������棩 ���ͣ�������
��8�֣��Ȼ�������ֵ��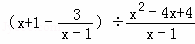 ������x���㷽�̣�x2+x��6=0��
������x���㷽�̣�x2+x��6=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�����ʡƽ��ɽ�о��꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
�������б����Ӧֵ���� ��
| 3.24 | 3.25 | 3.26 |
| -0.02 | 0.01 | 0.03 |
�жϹ���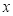 �ķ���
�ķ���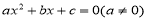 ��һ����
��һ����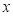 �ķ�Χ��
�ķ�Χ��
A�� ��3.24 B��3.24��
��3.24 B��3.24�� ��3.25
��3.25
C��3.25�� ��3.26 D��3.25��
��3.26 D��3.25�� ��3.26
��3.26
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com