
����Ŀ����ͼ����֪������y=ax2+2x+c��y�ύ�ڵ�A��0��6������x�ύ�ڵ�B��6��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮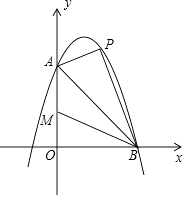
��1�������������ߵı���ʽ���䶥�����ꣻ
��2������P�ƶ��������ߵ�ʲôλ��ʱ��ʹ�á�PAB=75�㣬�����ʱ��P�����ꣻ
��3������P��A��������߶�AB�Ϸ������������յ�B�ƶ������ƶ��У���P�ĺ�������ÿ��1����λ���ȵ��ٶȱ䶯�����ͬʱ��M��ÿ��1����λ���ȵ��ٶ���AO���յ�O�ƶ�����P��M�ƶ��������յ�ʱֹͣ���������Ƶ��ƶ�t��ʱ�����ı���PAMB�����S����t�ĺ�������ʽ������tΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
���𰸡�
��1��
�⣺�������⣬��A��0��6����B��6��0�����������߽���ʽ�ɵ� ![]() �����
����� 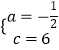 ��
��
�������ߵı���ʽΪy=�� ![]() x2+2x+6��
x2+2x+6��
��y=�� ![]() x2+2x+6=��
x2+2x+6=�� ![]() ��x��2��2+8��
��x��2��2+8��
�������ߵĶ�������Ϊ��2��8��
��2��
�⣺��ͼ1����P��PC��y���ڵ�C��
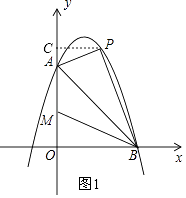
��OA=OB=6��
���OAB=45�㣬
�൱��PAB=75��ʱ����PAC=60�㣬
��tan��PAC= ![]() ����
���� ![]() =
= ![]() ��
��
��AC=m����PC= ![]() m��
m��
��P�� ![]() m��6+m����
m��6+m����
��P��������������߱���ʽ�ɵ�6+m=�� ![]() ��
�� ![]() m��2+2
m��2+2 ![]() m+6�����m=0��m=
m+6�����m=0��m= ![]() ��
�� ![]() ��
��
�����飬P��0��6�����A�غϣ��������⣬��ȥ��
�������P��������4�� ![]() ��
�� ![]() +
+ ![]() ��
��
��3��
�⣺������֧���ƶ�t��ʱ����P��t���� ![]() t2+2t+6����M��0��6��t����
t2+2t+6����M��0��6��t����
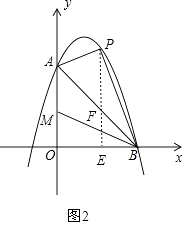
��ͼ2����PE��x���ڵ�E����AB�ڵ�F����EF=EB=6��t��
��F��t��6��t����
��FP= ![]() t2+2t+6����6��t��=��
t2+2t+6����6��t��=�� ![]() t2+3t��
t2+3t��
�ߵ�A��PE�ľ�����OE����B��PE�ľ������BE��
��S��PAB= ![]() FPOE+
FPOE+ ![]() FPBE=
FPBE= ![]() FP��OE+BE��=
FP��OE+BE��= ![]() FPOB=
FPOB= ![]() ������
������ ![]() t2+3t����6=��
t2+3t����6=�� ![]() t2+9t����S��AMB=
t2+9t����S��AMB= ![]() AMOB=
AMOB= ![]() ��t��6=3t��
��t��6=3t��
��S=S�ı���PAMB=S��PAB+S��AMB=�� ![]() t2+12t=��
t2+12t=�� ![]() ��t��4��2+24��
��t��4��2+24��
�൱t=4ʱ��S�����ֵ�����ֵΪ24
����������1����A��B���꣬���ô���ϵ��������������ߵı���ʽ����Ϊ����ʽ����ö������ꣻ��2����P��PC��y���ڵ�C������������á�PAC=60�㣬����AC=m����Rt��PAC�У��ɱ�ʾ��PC�ij����Ӷ�����m��ʾ��P�����꣬���������߽���ʽ�����m��ֵ���������P�����ꣻ��3����t�ɱ�ʾ��P��M�����꣬��P��PE��x���ڵ�E����AB�ڵ�F����ɱ�ʾ��F�����꣬�Ӷ�����t��ʾ��PF�ij����Ӷ��ɱ�ʾ����PAB�����������S�ı���PAMB=S��PAB+S��AMB �� �ɵõ�S����t�Ķ��κ��������ö��κ��������ʿ���������ֵ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ������C�ڡ�O�ϣ�����C��ֱ����AB���ӳ��߽��ڵ�P��AC=PC����COB=2��PCB��
��1����֤��PC�ǡ�O�����ߣ�
��2����֤��BC= ![]() AB��
AB��
��3����M�� ![]() ���е㣬CM��AB�ڵ�N����AB=4����MNMC��ֵ��
���е㣬CM��AB�ڵ�N����AB=4����MNMC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y= ![]() ��ͼ���ڵ�һ�����ڵ�A��4��2������y��ĸ����ύ�ڵ�B����OB=6��
��ͼ���ڵ�һ�����ڵ�A��4��2������y��ĸ����ύ�ڵ�B����OB=6�� 
��1������y= ![]() ��y=kx+b�Ľ���ʽ��
��y=kx+b�Ľ���ʽ��
��2����ֱ֪��AB��x���ཻ�ڵ�C���ڵ�һ�����ڣ���������y= ![]() ��ͼ����һ��P��ʹ��S��POC=9��
��ͼ����һ��P��ʹ��S��POC=9��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�AD=AC��AD��AC��E��AB���е㣬F��AC�ӳ�����һ�㣮
��1����ED��EF����֤��ED=EF��
��2���ڣ�1���������£���DC���ӳ�����FB���ڵ�P�����ж��ı���ACPE�Ƿ�Ϊƽ���ı��Σ���֤����Ľ��ۣ����Ȳ�ȫͼ�Σ��ٽ�𣩣�
��3����ED=EF��ED��EF��ֱ������ֱ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���̻���������Ӣ��ѧ���꼶����ͬѧ�������μ�ֲ���������ֲ����ʱ���ð�ͬѧֲ������IJ���������ͼ��ʾ�������ͳ��ͼ��Ϣ���ش��������⣺ 
��1�����꼶����ж�����ͬѧ��
��2������ͳ��ͼ�У�m= �� n= ��
��3������ͳ��ͼ�У��Լ���ֲ��2�õ���������Ӧ������Բ�ĽǵĶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AC��BD�ཻ�ڵ�O��O��AC���е㣬AD��BC��AC=8��BD=6���� 
��1����֤���ı���ABCD��ƽ���ı��Σ�
��2����AC��BD����ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��x+5��˫����y= ![]() ��x��0���ཻ��A��B���㣬��x���ཻ��C�㣬��BOC�������
��x��0���ཻ��A��B���㣬��x���ཻ��C�㣬��BOC������� ![]() ������ֱ��y=��x+5����ƽ��1����λ��������ֱ����˫����y=
������ֱ��y=��x+5����ƽ��1����λ��������ֱ����˫����y= ![]() ��x��0���Ľ����У� ��
��x��0���Ľ����У� �� 
A.0��
B.1��
C.2��
D.0������1������2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=��x2+2x�Ķ���ΪA��ֱ��y=x��2�������߽���B��C���㣮

��1����A��B��C��������ꣻ
��2����CD��x���ڵ�D����֤����ODC�ס�ABC��
��3������PΪ�������ϵ�һ�����㣬����P��PM��x���ڵ�M�����Ƿ��ڳ�C���������λ�õĵ㣬ʹ��O��P��MΪ��������������ABC���ƣ������ڣ������������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y=ax2+bx+4��ͼ���A����1��0����B��4��0�����㣬��y�ύ�ڵ�C����ֱ��BC������P�ӵ�C��������ÿ�� ![]() ����λ���ȵ��ٶ���CB���B�˶����˶�ʱ��Ϊt�룬����P���B�غ�ʱֹͣ�˶���
����λ���ȵ��ٶ���CB���B�˶����˶�ʱ��Ϊt�룬����P���B�غ�ʱֹͣ�˶���
��1���������ߵı���ʽ��
��2����ͼ2����t=1ʱ����S��ACP�������
��3����ͼ3������P��x�������߷ֱ�x�ᣬ��������E��F���㣮
����PF�ij��ȹ���t�ĺ�������ʽ�������PF�ij��ȵ����ֵ��
������CF������PCF��CF�۵��õ���P��CF����tΪ��ֵʱ���ı���PFP��C�����Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com