
����Ŀ����ͼ1��������y=ax2+bx+4��ͼ���A����1��0����B��4��0�����㣬��y�ύ�ڵ�C����ֱ��BC������P�ӵ�C��������ÿ�� ![]() ����λ���ȵ��ٶ���CB���B�˶����˶�ʱ��Ϊt�룬����P���B�غ�ʱֹͣ�˶���
����λ���ȵ��ٶ���CB���B�˶����˶�ʱ��Ϊt�룬����P���B�غ�ʱֹͣ�˶���
��1���������ߵı���ʽ��
��2����ͼ2����t=1ʱ����S��ACP�������
��3����ͼ3������P��x�������߷ֱ�x�ᣬ��������E��F���㣮
����PF�ij��ȹ���t�ĺ�������ʽ�������PF�ij��ȵ����ֵ��
������CF������PCF��CF�۵��õ���P��CF����tΪ��ֵʱ���ı���PFP��C�����Σ�
���𰸡�
��1��
�⣺��������y=ax2+bx+4��ͼ���A����1��0����B��4��0�����㣬
�� ![]() ����ã�
����ã� ![]() ��
��
�������ߵı���ʽΪy=��x2+3x+4��
��2��
�⣺��x=0����y=4��
����C��������0��4����
��BC= ![]() =4
=4 ![]() ��
��
��ֱ��BC�Ľ���ʽΪy=kx+4��
�ߵ�B������Ϊ��4��0����
��0=4k+4�����k=��1��
��ֱ��BC�Ľ���ʽΪy=��x+4��
��t=1ʱ��CP= ![]() ��
��
��A����1��0����ֱ��BC�ľ���h= ![]() =
= ![]() =
= ![]() ��
��
S��ACP= ![]() CPh=
CPh= ![]() ��
�� ![]() ��
�� ![]() =
= ![]() ��
��
��3��
�⣺�١�ֱ��BC�Ľ���ʽΪy=��x+4��
��CP= ![]() t��OE=t����P��t����t+4����F��t����t2+3t+4������0��t��4��
t��OE=t����P��t����t+4����F��t����t2+3t+4������0��t��4��
PF=��t2+3t+4������t+4��=��t2+4t����0��t��4����
��t=�� ![]() =2ʱ��PFȡ���ֵ�����ֵΪ4��
=2ʱ��PFȡ���ֵ�����ֵΪ4��
�ڡߡ�PCF��CF�۵��õ���P��CF��
��PC=P��C��PF=P��F��
���ı���PFP��C������ʱ��ֻ��PC=PF��
�� ![]() t=��t2+4t��
t=��t2+4t��
��ã�t1=0����ȥ����t2=4�� ![]() ��
��
�ʵ�t=4�� ![]() ʱ���ı���PFP��C�����Σ�
ʱ���ı���PFP��C�����Σ�
����������1����A��B���������뺯������ʽ�У����ɵõ�����a��b�Ķ�Ԫһ�η��̣��ⷽ�̼��ɵó����ۣ���2����x=0�ɵó�C������꣬���ֱ��BC����ʽy=kx+4������B����������kֵ����������������A��ֱ��BC�ľ����������ε���������ɵó����ۣ���3������ֱ��BC�Ľ���ʽΪy=��x+4�ɵ�֪OE= ![]() CP�����P��F������꣬��F��������ꩁP��������꼴�ɵó�PF�ij��ȹ���t�ĺ�������ʽ����϶��κ��������ʼ��������ֵ���⣻���ɷ�ת���Կ�֪PC=P��C��PF=P��F�����ı���PFP��C�����Σ�����PC=PF���ɴ˵ó�����t�Ķ�Ԫһ�η��̣��ⷽ�̼��ɵó����ۣ�
CP�����P��F������꣬��F��������ꩁP��������꼴�ɵó�PF�ij��ȹ���t�ĺ�������ʽ����϶��κ��������ʼ��������ֵ���⣻���ɷ�ת���Կ�֪PC=P��C��PF=P��F�����ı���PFP��C�����Σ�����PC=PF���ɴ˵ó�����t�Ķ�Ԫһ�η��̣��ⷽ�̼��ɵó����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+2x+c��y�ύ�ڵ�A��0��6������x�ύ�ڵ�B��6��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮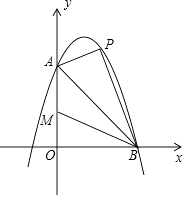
��1�������������ߵı���ʽ���䶥�����ꣻ
��2������P�ƶ��������ߵ�ʲôλ��ʱ��ʹ�á�PAB=75�㣬�����ʱ��P�����ꣻ
��3������P��A��������߶�AB�Ϸ������������յ�B�ƶ������ƶ��У���P�ĺ�������ÿ��1����λ���ȵ��ٶȱ䶯�����ͬʱ��M��ÿ��1����λ���ȵ��ٶ���AO���յ�O�ƶ�����P��M�ƶ��������յ�ʱֹͣ���������Ƶ��ƶ�t��ʱ�����ı���PAMB�����S����t�ĺ�������ʽ������tΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=x2+bx��ͼ����ͼ���Գ���Ϊֱ��x=1��������x��һԪ���η���x2+bx��t=0��tΪʵ�����ک�1��x��4�ķ�Χ���н⣬��t��ȡֵ��Χ�ǣ� �� 
A.t�ݩ�1
B.��1��t��3
C.��1��t��8
D.3��t��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�O������ԭ�㣬ABCD�Ķ���A������Ϊ����2��0������D������Ϊ��0��2 ![]() ������B��x����������ϣ���EΪ�߶�AD���е㣬����E��ֱ��l��x�ύ�ڵ�F��������DC���ڵ�G��
������B��x����������ϣ���EΪ�߶�AD���е㣬����E��ֱ��l��x�ύ�ڵ�F��������DC���ڵ�G��
��1�����DCB�Ķ�����
��2������F������Ϊ����4��0��ʱ�����G�����ꣻ
��3������OE����OE����ֱ��Ϊ�Գ��ᣬ��OEF����ԳƱ任��õ���OEF'����ֱ��EF'������DC�Ľ���ΪH��
��ͼ2������G�ڵ�H�����ʱ����֤����DEG�ס�DHE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ҫ����м��㣺
��1�����㣺|�� ![]() |��
|�� ![]() +2sin60��+��
+2sin60��+�� ![]() ����1+��2��
����1+��2�� ![]() ��0
��0
��2���Ȼ�������ֵ�� ![]() �£�1��
�£�1�� ![]() ��������a=
��������a= ![]() ��2��
��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ڡ�O�ϣ���ABC��ƽ������AC�ཻ�ڵ�D�����O����A�������ཻ�ڵ�E�� 
��1����ACB=�㣬�����ǣ���
��2�������EAD����״����֤����IJ��룻
��3����AB=8��AD=6����BD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������ѧ����ҵ�������ƶ���С����ҵ���Ż����ߣ�����С����ҵӦ�˶�����ij��ͳ���˸���2015��1��5����ע��С����ҵ������������������Ƴ���ͼ���ֲ�������ͳ��ͼ�� 
��1��ij��2015��1��5�·���ע��С����ҵһ���ң��뽫����ͳ��ͼ����������
��2������2015��3����ע��С����ҵ�У�ֻ��2������ֳ��ҵ���ִ�3����ע���С����ҵ�������ȡ2����ҵ�˽��侭Ӫ����������б�����״ͼ�ķ����������ȡ��2����ҵǡ�ö�����ֳ��ҵ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������³�鷢�������ij������չ�װ��Ļ��������Ա��������������ͼ�Ǹ��������ֵ�Ա������������ͳ��ͼ����ô���ξ��Ǯ������������λ���ֱ��ǣ�������
A.100Ԫ��100Ԫ
B.100Ԫ��200Ԫ
C.200Ԫ��100Ԫ
D.200Ԫ��200Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AC=BC��б��AB=2��O��AB���е㣬��OΪԲ�ģ��߶�OC�ij�Ϊ�뾶��Բ�Ľ�Ϊ90�������OEF����EF������C����ͼ����Ӱ���ֵ����Ϊ �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com