
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是 ![]() 的中点,CM交AB于点N,若AB=4,求MNMC的值.
的中点,CM交AB于点N,若AB=4,求MNMC的值.
【答案】
(1)
证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.
即OC⊥CP,
∵OC是⊙O的半径.
∴PC是⊙O的切线.
(2)
证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC= ![]() AB.
AB.
;
证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC= ![]() AB.
AB.
;证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC= ![]() AB.
AB.
(3)
解:连接MA,MB,
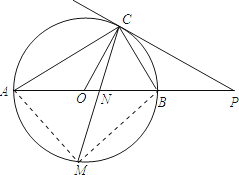
∵点M是 ![]() 的中点,
的中点,
∴ ![]() ,
,
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴ ![]() .
.
∴BM2=MNMC.
又∵AB是⊙O的直径, ![]() ,
,
∴∠AMB=90°,AM=BM.
∵AB=4,
∴BM= ![]() .
.
∴MNMC=BM2=8.
【解析】(1)已知C在圆上,故只需证明OC与PC垂直即可;根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP;故PC是⊙O的切线;(2)AB是直径;故只需证明BC与半径相等即可;(3)连接MA,MB,由圆周角定理可得∠ACM=∠BCM,进而可得△MBN∽△MCB,故BM2=MNMC;代入数据可得MNMC=BM2=8.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数y=﹣ ![]() 的图象上一点,直线y=﹣
的图象上一点,直线y=﹣ ![]() 与反比例函数y=﹣
与反比例函数y=﹣ ![]() 的图象在第四象限的交点为点B.
的图象在第四象限的交点为点B.
(1)求直线AB的解析式;
(2)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转一定角度后得△EDC,点D在AB边上,斜边DE交AC于点F,则图中阴影部分面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,则下列结论:①b2﹣4ac<0;②a﹣b+c>0;③abc>0;④b=2a中,正确的结论的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1 , 则下列结论:
①b>0;②a﹣b+c<0;③阴影部分的面积为4;④若c=﹣1,则b2=4a.
正确的是( )
A.①③
B.②③
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市一中准备组织学生及学生家长到武汉大学参观体验,为了便于管理,所有人员到武汉必须乘坐在同一列动车上;根据报名人数,若都买 一等座单程火车票需2556元,若都买二等座单程火车票且花钱最少,则需1530元;已知学生家长与教师的人数之比为2:1,安陆到武汉的动车票价格(动 车学生票只有二等座可以打6折)如下表所示:
(1)参加参观体验的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加参观体验的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买单程火车票的总费用至少是多少钱?最多是多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+2x+c与y轴交于点A(0,6),与x轴交于点B(6,0),点P是线段AB上方抛物线上的一个动点.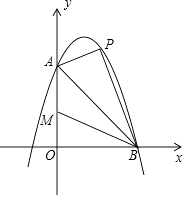
(1)求这条抛物线的表达式及其顶点坐标;
(2)当点P移动到抛物线的什么位置时,使得∠PAB=75°,求出此时点P的坐标;
(3)当点P从A点出发沿线段AB上方的抛物线向终点B移动,在移动中,点P的横坐标以每秒1个单位长度的速度变动,与此同时点M以每秒1个单位长度的速度沿AO向终点O移动,点P,M移动到各自终点时停止,当两个移点移动t秒时,求四边形PAMB的面积S关于t的函数表达式,并求t为何值时,S有最大值,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com