
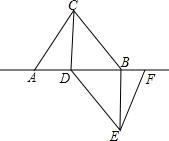
 ��ABC�͡�DEF���DZ߳�Ϊ6cm�ĵȱ������Σ���A��D��B��F��ͬһֱ���ϣ�����CD��BF��
��ABC�͡�DEF���DZ߳�Ϊ6cm�ĵȱ������Σ���A��D��B��F��ͬһֱ���ϣ�����CD��BF������ ��1���ɡ�ABC�͡�DEF�������߳�Ϊ6cm�ĵȱ������Σ��ó�BC=DF���ɡ�ACD=��FDE=60�㣬�ó�BC��DE��֤���ı���BCDE��ƽ���ı��Σ�
��2����a��������һ���ڱ���ȵ��ı��������μ��ɵõ����ۣ�
��b��������һ������ֱ�ǵ�ƽ���ı����Ǿ��μ��ɵõ����ۣ��ɹ��ɶ������BE������������ε������
��� ��1��֤�����ߡ�ABC�͡�DEF�������߳�Ϊ6cm�ĵȱ������Σ�
��BC=DE����ABC=��FDE=60�㣬
��BC��DE��
���ı���BCDE��ƽ���ı��Σ�
��2���⣺��a����t=2��ʱ��?BCDE�����Σ�
��ʱA��D�غϣ�
��CD=DE��
��?ADEC������
��b����ƽ���ı���BCDE�Ǿ��Σ����CDE=90�㣬��ͼ��ʾ��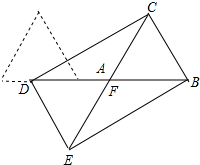
���CDB=90��-60��=30��
ͬ����DCA=30��=��CDB��
��AC=AD��
ͬ��FB=EF��
��F��A�غϣ�
��t=��6+2����1=8�룬
�൱t=8��ʱ��ƽ���ı���BCDE�Ǿ��Σ�
�ɹ��ɶ����ã�BE=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$��
�����BCDE�����=BC•BE=6��6$\sqrt{3}$=36$\sqrt{3}$��
���� �������ı����ۺ���Ŀ�������˵ȱ������ε����ʡ�ƽ���ı��ε��ж������ε��ж������ε��ж������ɶ�����֪ʶ�������ۺ���ǿ����һ���Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
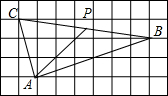 ��ͼ������������ı߳�Ϊ1����A��B��C������ĸ���ϣ���PΪBC���е㣬��AP=$\frac{5\sqrt{2}}{2}$��
��ͼ������������ı߳�Ϊ1����A��B��C������ĸ���ϣ���PΪBC���е㣬��AP=$\frac{5\sqrt{2}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com