练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，⊙O是△ABC的外接圆，∠A=40°，则∠OCB等于（　　）

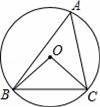
    A．60° B．50° C．40° D．30°


    B【考点】圆周角定理．

    【分析】由⊙O是△ABC的外接圆，∠A=40°，然后由圆周角定理，即可求得∠BOC的度数，又由等腰三角形的性质，即可求得∠OCB的度数．

    【解答】解：∵⊙O是△ABC的外接圆，∠A=40°，

    ∴∠BOC=2∠A=80°，

    ∵OB=OC，

    ∴∠OCB==50°．

    故选B．

    【点评】此题考查了圆周角定理与等腰三角形的性质．此题难度不大，注意掌握数形结合思想的应用．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若ab＞0，则一次函数y=ax+b与反比例函数y=在同一坐标系数中的大致图象是（　　）

    A．  B．      C．  D．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


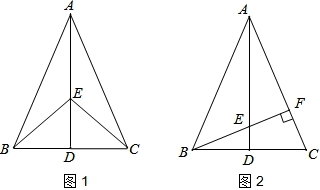
    如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．

    （1）求证：BE=CE；

    （2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其它条件不变．求证：△AEF≌△BCF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    化简+，并代入原式有意义的数进行计算．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


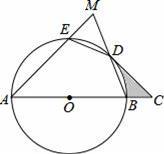
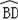
    如图，AB是⊙O的直径， =，连接ED、BD，延长AE交BD的延长线于点M，过点D作⊙O的切线交AB的延长线于点C．

    （1）若OA=CD=2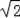，求阴影部分的面积；

    （2）求证：DE=DM．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平行四边形ABCD中，E为CD上一点，连接AE、BE、BD，且AE、BD交于点F，S△DEF：S△ABF=4：25，则DE：EC=（　　）

    A．2：3 B．2：5 C．3：5 D．3：2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：

    x

    …

    ﹣2

    ﹣1

    0

    1

    2

    …

    y

    …

    0

    4

    6

    6

    4

    …

    从上表可知，下列说法正确的个数是（　　）

    ①抛物线与x轴的一个交点为（﹣2，0）；②抛物线与y轴的交点为（0，6）；③抛物线的对称轴是x=1；④在对称轴左侧y随x增大而增大．

    A．1    B．2    C．3    D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若AD//BE，且∠ACB=90°，∠CBE=30°，

    则∠CAD的度数为（    ）

    A、30°          B、40°

     C、50°          D、60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某校为了了解本校七年级学生课外阅读的喜好，随机抽取该校七年级部分学生进行问卷调査（每人只选一种书籍）．下图是整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

    （1）这次活动一共调查了　　　　　　名学生；

    （2）在扇形统计图中，“其他”所在扇形的圆心角等于　　　　　　度；

    （3）补全条形统计图；

    （4）若该年级有600名学生，请你估计该年级喜欢“科普常识”的学生人数约是　　　　　　．

    　

    查看答案和解析>>

    同步练习册答案