
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )


A.2:3 B.2:5 C.3:5 D.3:2
A【考点】相似三角形的判定与性质;三角形的面积;平行四边形的性质.
【专题】探究型.
【分析】先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF,再根据S△DEF:S△ABF=4:10:25即可得出其相似比,由相似三角形的性质即可求出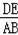
 的值,由AB=CD即可得出结论.
的值,由AB=CD即可得出结论.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAB=∠DEF,∠AFB=∠DFE,
∴△DEF∽△BAF,
∵S△DEF:S△ABF=4:25,
∴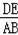
 =
=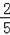
 ,
,
∵AB=CD,
∴DE:EC=2:3.
故选A.
【点评】本题考查的是相似三角形的判定与性质及平行四边形的性质,熟知相似三角形边长的比等于相似比,面积的比等于相似比的平方是解答此题的关键.


科目:初中数学 来源: 题型:
体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢后,足球踢到了小华处的概率是多少(用树状图表示或列表说明);
(2)如果踢三次后,球踢到了小明处的可能性最小,应从谁开始踢?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
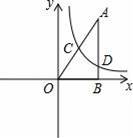
如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=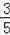
 ,反比例函数y=
,反比例函数y=
 (x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .
(x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .

查看答案和解析>>
科目:初中数学 来源: 题型:
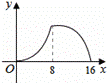
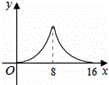
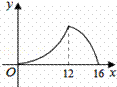
如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB
上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,
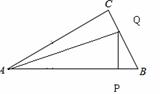 设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
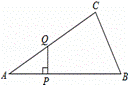
① ②
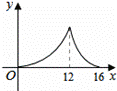
A、 B 、 C、 D、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com