
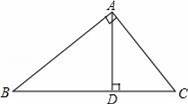
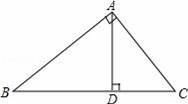
如图,Rt△ABC中,∠A=90°,AD⊥BC于点D,若BD:CD=3:2,则tanB=( )

A.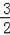
 B.
B.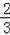
 C.
C.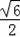
 D.
D.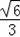

D【考点】相似三角形的判定与性质;锐角三角函数的定义.
【分析】首先证明△ABD∽△ACD,然后根据BD:CD=3:2,设BD=3x,CD=2x,利用对应边成比例表示出AD的值,继而可得出tanB的值.
【解答】解:在Rt△ABC中,
∵AD⊥BC于点D,
∴∠ADB=∠CDA,
∵∠B+∠BAD=90°,∠BAD+∠DAC=90°,
∴∠B=∠DAC,
∴△ABD∽△CAD,
∴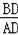
 =
=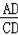
 ,
,
∵BD:CD=3:2,
设BD=3x,CD=2x,
∴AD=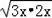
 =
=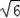
 x,
x,
则tanB=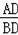
 =
=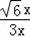
 =
=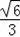
 .
.
故选D.

【点评】本题考查了相似三角形的判定与性质及锐角三角函数的定义,难度一般,解答本题的关键是根据垂直证明三角形的相似,根据对应边成比例求边长.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
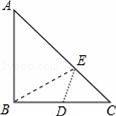
如图Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为( )

A.2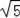
 B.2
B.2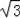
 C.2
C.2
 +2 D.2
+2 D.2
 +2
+2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )


A.2:3 B.2:5 C.3:5 D.3:2
查看答案和解析>>
科目:初中数学 来源: 题型:
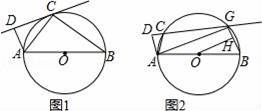
如图1,AB为⊙O的直径,C为⊙O上一点,作AD⊥CD,垂足为D.
(1)若直线CD与⊙O相切于点C,求证:△ADC∽△ACB;
(2)如果把直线CD向下平行移动,如图2,直线CD交⊙O于C、G两点,若题目中的其他条件不变,tan∠DAC=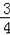
 ,AB=10,求圆心O到GB的距离OH的长.
,AB=10,求圆心O到GB的距离OH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com