
体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢后,足球踢到了小华处的概率是多少(用树状图表示或列表说明);
(2)如果踢三次后,球踢到了小明处的可能性最小,应从谁开始踢?请说明理由.
【考点】列表法与树状图法.
【专题】数形结合;分类讨论.
【分析】(1)列举出所有情况,看足球踢到了小华处的情况数占所有情况数的多少即可;
(2)可设球从小明处先开始踢,得到3次踢球回到小明处的概率,进而根据树状图可得球从其他2位同学处开始,3次踢球回到小明处的概率,比较可得可能性最小的方案.
【解答】解:(1)如图:
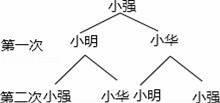

∴P(足球踢到小华处)=

(2)应从小明开始踢如图:
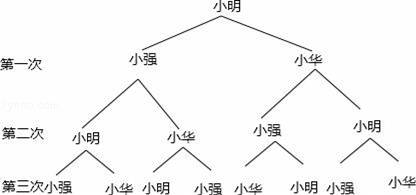

若从小明开始踢,P(踢到小明处)=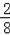
 =
=

同理,若从小强开始踢,P(踢到小明处)=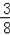

若从小华开始踢,P(踢到小明处)=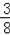
 (理由3分)
(理由3分)
【点评】考查用列树状图的方法解决概率问题;分类得到3次踢球踢到小明处的情况数是解决本题的难点;用到的知识点为:概率等于所求情况数与总情况数之比.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
如图Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为( )
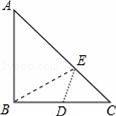

A.2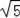
 B.2
B.2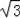
 C.2
C.2
 +2 D.2
+2 D.2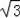
 +2
+2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )


A.2:3 B.2:5 C.3:5 D.3:2
查看答案和解析>>
科目:初中数学 来源: 题型:
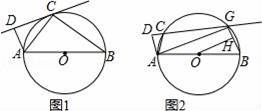
如图1,AB为⊙O的直径,C为⊙O上一点,作AD⊥CD,垂足为D.
(1)若直线CD与⊙O相切于点C,求证:△ADC∽△ACB;
(2)如果把直线CD向下平行移动,如图2,直线CD交⊙O于C、G两点,若题目中的其他条件不变,tan∠DAC=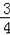
 ,AB=10,求圆心O到GB的距离OH的长.
,AB=10,求圆心O到GB的距离OH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com