练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．
    （1）当∠BQD=30°时，求AP的长；
    （2）证明：在运动过程中，点D是线段PQ的中点；
    （3）当运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．

    分析 （1）先判断出∠QPC是直角，再利用含30°的直角三角形的性质得出QC=2PC，建立方程求解决即可；
    （2）先作出PF∥BC得出∠PFA=∠FPA=∠A=60°，进而判断出△DQB≌△DPF得出DQ=DP即可得出结论；
    （3）利用等边三角形的性质得出EF=$\frac{1}{2}$AF，借助DF=DB，即可得出DF=$\frac{1}{2}$BF，最后用等量代换即可．

    解答 （1）解：设AP=x，则BQ=x，
    ∵∠BQD=30°，∠C=60°，
    ∴∠QPC=90°，
    ∴QC=2PC，即x+6=2（6-x），
    解得x=2，
    即AP=2．
    （2）证明：如图，

    过P点作PF∥BC，交AB于F，
    ∵PF∥BC，
    ∴∠PFA=∠FPA=∠A=60°，
    ∴PF=AP=AF，
    ∴PF=BQ，
    又∵∠BDQ=∠PDF，∠DBQ=∠DFP，
    ∴△DQB≌△DPF，
    ∴DQ=DP即D为PQ中点，
    （3）运动过程中线段ED的长不发生变化，是定值为3，
    理由：∵PF=AP=AF，PE⊥AF，
    ∴$EF=\frac{1}{2}AF$，
    又∵△DQB≌△DPF，
    ∴$DF=DB，即DF=\frac{1}{2}BF$，
    ∴$ED=EF+DF=\frac{1}{2}（AF+BF）=\frac{1}{2}AB=3$．

    点评 此题是三角形综合题，主要考查了含30°的直角三角形的性质，等边三角形的性质，全等三角形的判定和性质，判断出△DQB≌△DPF是解本题的关键，作出辅助线是解本题的难点，是一道比较简单的中考常考题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．当x=-$\frac{1}{2}$时，求多项武3-2x2+3x+3x2-5x-7的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．x=-1是下列哪个方程的解（　　）
    A．x-5=6B．$\frac{1}{2}$x+6=6C．3x+1=4D．4x+4=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

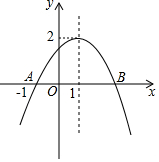    6．二次函数y=ax2+bx+c（a≠0）的图如图所示根据图答下列问题：
    （1）B点坐标为（3，0）；
    （2）方程ax2+bx+c=0的两个根为x1=-1，x2=3；
    （3）不等式ax2+bx+c＜0的解集为x＜-1或x＞3；
    （4）y随x的增大而减小的自变量x的取值范围为x＞1；
    （5）若方程ax2+bx+c=k-1有两个不相等的实数根，则k的取值范围为k＜3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列命题中，真命题的个数（　　）
    （1）⊙O的半径为5，点P在直线l上，且OP=5，则直线l与⊙O相切
    （2）在Rt△ABC中，∠C=90°，AC=5，BC=12，则△ABC的外接圆半径为6.5
    （3）正多边形都是轴对称图形，也都是中心对称图形
    （4）三角形的外心到三角形各边的距离相等．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．将抛物线y=2x2向左平移2个单位，再向上平移3个单位得到的抛物线解析式是（　　）
    A．y=2（x+2）2+3B．y=2（x-2）2-3C．y=2（x+2）2-3D．y=2（x-2）2+3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．在数轴上，表示-17的点与表示-10的点之间的距离是（　　）
    A．27个单位长度B．-27个单位长度C．7个单位长度D．-7个单位长度

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．已知二次函数y=ax2+bx+c的图象如图所示，有以下结论：
    ①abc＜0，②a-b+c＜0，③2a=b，④b2＞4ac，⑤若点（-2，y1）和（-$\frac{1}{3}$，y2）在该图象上，则y1＞y2．
    其中正确的结论是①②④（填入正确结论的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．把方程2x2-3x+1=0变形为（x+a）2=b的形式，正确的变形是（　　）
    A．（x-$\frac{3}{2}$）2=16B．（x-$\frac{3}{4}$）2=$\frac{1}{16}$C．2（x-$\frac{3}{4}$）2=$\frac{1}{16}$D．2（x-$\frac{3}{2}$）2=16

    查看答案和解析>>

    同步练习册答案