
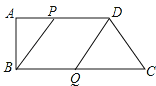
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=16cm,BC=22cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.

(1)当t为多少时,四边形ABQP成为矩形?
(2)四边形PBQD是否能成为菱形?若能,求出t的值;若不能,请说明理由,并探究如何改变Q点的速度(匀速运动),使四边形PBQD在某一时刻为菱形,求点Q的速度.
【答案】(1)t=![]() s;(2)2cm/s.
s;(2)2cm/s.
【解析】
试题分析:(1)因为∠B=90°,AP∥BQ,由矩形的判定可知当AP=BQ时,四边形ABQP成为矩形;
(2)因为PD∥BQ,当PD=BQ=BP时,四边形PBQD能成为菱形,先由PD=BQ求出运动时间t的值,再代入求BP,发现BP≠PD,判断此时四边形PBQD不能成为菱形;设Q点的速度改变为vcm/s时,四边形PBQD在时刻t为菱形,根据PD=BQ=BP列出关于v、t的方程组,解方程组即可求出点Q的速度.
试题解析:(1)∵∠B=90°,AP∥BQ,
∴当AP=BQ时,四边形ABQP成为矩形,
此时有t=22-3t,解得t=![]() .
.
∴当t=![]() s时,四边形ABQP成为矩形;
s时,四边形ABQP成为矩形;
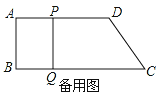
(2)四边形PBQD不能成为菱形.理由如下:
∵PD∥BQ,
∴当PD=BQ=BP时,四边形PBQD能成为菱形.
由PD=BQ,得16-t=22-3t,解得t=3,
当t=3时,PD=BQ=13,BP=![]() ,
,
∴四边形PBQD不能成为菱形;
如果Q点的速度改变为vcm/s时,能够使四边形PBQD在时刻ts为菱形,
由题意,得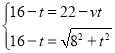 ,解得
,解得![]() .
.
故点Q的速度为2cm/s时,能够使四边形PBQD在某一时刻为菱形.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 正数的绝对值是负数 B. 任何一个有理数都有相反数
C. π的相反数是―3.14 D. 符号不同的两个数互为相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时应假设( )
A. 三角形中有一个内角小于或等于60° B. 三角形中有两个内角小于或等于60°
C. 三角形中有三个内角小于或等于60° D. 三角形中没有一个内角小于或等于60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铅笔每支售价0.20元,在平面直角坐标系内表示小明买1支到10支铅笔需要花费的钱数的图像是( )
A. 一条直线 B. 一条射线 C. 一条线段 D. 10个不同的点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com