
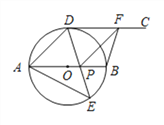
【题目】如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D.连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①若DF=AP,当∠DAE=_________时,四边形ADFP是菱形;
②若BF⊥DF,当∠DAE=_________时,四边形BFDP是正方形.
【答案】(1)证明见解析;(2)① 67.5°,②90°.
【解析】试题分析:(1)连接OD,根据切线的性质可得OD⊥CD,再由圆周角定理可得∠AOD=90°,即可得证;
(2)①根据菱形的性质和等腰三角形的性质求得∠ADP,在△ADE中利用三角形的内角和定理求得∠DAE的度数即可;
②判断四边形BFDP是正方形时,当DE是⊙O的直径即可求得∠DAE.
试题解析:(1)连接OD,∵射线DC切⊙O于点D,
∴OD⊥CD,
∵∠AED = 45°,
∴∠AOD = 2∠AED = 90°,
即∠ODF = ∠AOD ,
∴CD∥AB;
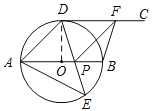
(2)①∵四边形ADFP是菱形,∴AD=AP,
∵在Rt△AOD中,OA=OD,∴∠DAO=45°,∴∠ADP=∠APD=(180°-45°)÷2=67.5°,
∴在△ADE中,∠DAE=180°-∠ADE-∠AED=180°-67.5°-45°=67.5°,
故答案为:67.5°;
②当BF⊥DF,DE⊥AB是四边形BFDP是正方形,
由题意可知,DE⊥AB时,DE经过⊙O的圆心,∴DE是⊙O的直径,∴∠DAE=90°,
故答案为:90°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某地区的一次人口抽样统计分析中,各年龄段(年龄取整数)的人数如下表:
年龄段 | 0~9 | 10~19 | 20~29 | 30~39 | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 |
人数 | 9 | 11 | 17 | 18 | 17 | 12 | 8 | 6 | 2 |
请根据此表回答下列问题:
(1)这次抽查的样本个体的数目是_____;
(2)样本中年龄在60岁以上(含60岁)的频率是_____;
(3)样本中年龄的中位数落在表中给出的哪个年龄段内?
(4)如果该地区现有人口80000人,为了关注人口老龄化问题,请估算该地区60岁以上(含60岁)的人口数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).

(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,下列条件中,不能使四边形DBCE成为菱形的是( )
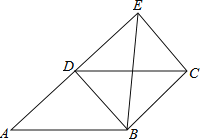
A.AB=BEB.BE⊥DCC.∠ABE=90°D.BE平分∠DBC
查看答案和解析>>
科目:初中数学 来源: 题型:
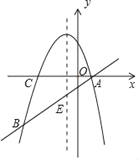
【题目】如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.
(1)求抛物线的解板式.
(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.
(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
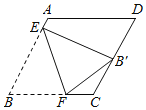
【题目】在菱形ABCD中,AB=2,∠BAD=120°,点E,F分别是边AB,BC边上的动点,沿EF折叠△BEF,使点B的对应点B’始终落在边CD上,则A、E两点之间的最大距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
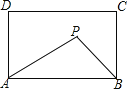
【题目】如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com