
【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|,利用数形结合思想回答下列问题:![]()
(1)数轴上表示2和10两点之间的距离是____,数轴上表示2和-10两点之间的距离是
____;
(2)数轴上,x和-2两点之间的距离是|x+2|_____;
(3)若x表示一个有理数,则|x-1+|x+2|有最小值吗?若有,请求出最小值,若没有,写出理由.
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABC的平分线交AD于点E,过点D作BE的平行线交于BC于F.
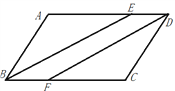
(1)求证:△ABE≌△CDF;
(2)若AB=6,BC=8,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( )
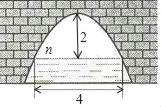
A. 1 m B. 2 m C. 3 m D. 6 m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜种植基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.
(1)改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元?
(2)已知改造1个甲种型号大棚的时间是5天,改造1个乙种型号大概的时间是3天,该基地计划改造甲、乙两种蔬菜大棚共8个,改造资金最多能投入128万元,要求改造时间不超过35天,请问有几种改造方案?哪种方案基地投入资金最少,最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,若直线DF垂直平分AB,垂足为点E,连接BF,CE,且BC=2,下面四个结论:①BF=![]() ;②∠CBF=45°;③△BEC的面积=△FBC的面积;④△ECD的面积为
;②∠CBF=45°;③△BEC的面积=△FBC的面积;④△ECD的面积为![]() ,其中正确的结论有( )
,其中正确的结论有( )
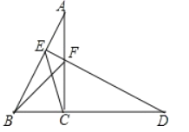
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.我市区机抽取了部分家庭,调查每月用于信息消费的金额,数据整理成如图所示的不完整统计图.已知A、B两组户数直方图的高度比为1:5,请结合图中相关数据回答下列问题:

(1)A组的频数是 ,本次调查样本的容量是 ;
(2)补全直方图(需标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额不少于300元的户数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:
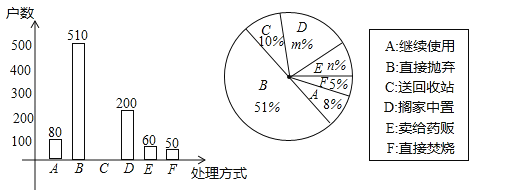
①m= ,n= ;
②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com