
【题目】如图,在ABCD中,∠ABC的平分线交AD于点E,过点D作BE的平行线交于BC于F.
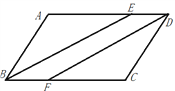
(1)求证:△ABE≌△CDF;
(2)若AB=6,BC=8,求DE的长.
【答案】(1)证明见解析(2)2
【解析】(1)首先由平行四边形的性质可得AD∥BC,AB=CD;∠A=∠C,再由条件利用SAS定理可判定△ABE≌△CDF;(2)由(1)可知 ∠EBF=∠AEB由平行线的性质和角平分线得出∠AEB=∠ABE,即可得出结果.
解:(1)证明:法一:
∵四边形ABCD是平行四边形
∴AD∥BC,AD=BC,∠A=∠C,,
∵BE∥DF,

∴四边形BEDF是平行四边形,
∴DE=BF,
∴AD-DE=BC-BF,
即:AE=CF,
∴△ABE≌△CDF(SAS).
法二:∵BE//FD ∴∠EBF=∠DFC
∵AD//BC ∴∠EBF=∠AEB
∴∠AEB=∠DFC
在ABCD中,∵∠A=∠C,AB=CD
∴ △ABE≌△CDF
(2)由(1)可知 ∠EBF=∠AEB
又∵BE平分∠EBF
∴∠EBF=∠ABE
∴∠AEB=∠ABE
∴AE=AB=6
又∵BC=AD=8
∴DE=2
“点睛”本题考查了平行四边形的判定与性质、等腰三角形的判定;熟记平行四边形的性质,证出AE=AB是解决(2)的关键.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱剩余油量为30升.(假设行驶过程中汽车的耗油量是均匀的.)
(1)写出用行驶路程x(千米)来表示剩余油量Q(升)的代数式;
(2)当x=300千米时,求剩余油量Q的值;
(3)当油箱中剩余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,抛物线与x轴交于A(﹣1,0),B(3,0),顶点为D(1,﹣4),点P为y轴上一动点.
(1)求抛物线的解析式;
(2)在y轴的负半轴上是否存在点P,使△BDP是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(3)如图2,点![]() 在抛物线上,求
在抛物线上,求![]() 的最小值.
的最小值.
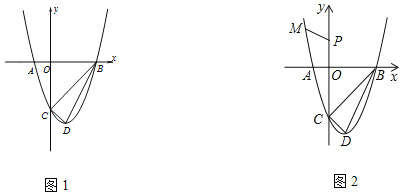
查看答案和解析>>
科目:初中数学 来源: 题型:
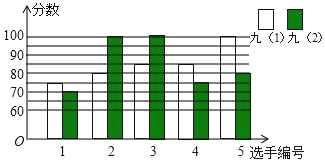
【题目】为选拔优秀选手参加瑶海区第八届德育文化艺术节“诵经典”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示
(1)根据图示填写下表
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 |
| 85 |
九(2) |
| 80 |
|
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班五名选手的成绩较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(-3)-(-2)+(-4)
(2)(-![]() )-(-
)-(-![]() )-|-
)-|-![]() |-(-
|-(-![]() )
)
(3)-23÷![]() ×(-
×(-![]() )2
)2
(4)(![]() )×(-36)
)×(-36)
(5)-14-![]() ×
×![]()
(6)(-1)4+5÷(-![]() )×(-6)
)×(-6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN.

(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;
(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系 ;
(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘一辆汽车沿公路检修线路,约定向东走为正,向西走为负。某天从A地出发到收工时,行走记录(长度单位:千米)为:+15,-2,+5,-1,+10,-3。
⑴问收工时,检修小组在A处的哪一边,距A地多远?
⑵若汽车每千米的耗油为![]() 升,求从出发到收工共耗油多少升?
升,求从出发到收工共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|,利用数形结合思想回答下列问题:![]()
(1)数轴上表示2和10两点之间的距离是____,数轴上表示2和-10两点之间的距离是
____;
(2)数轴上,x和-2两点之间的距离是|x+2|_____;
(3)若x表示一个有理数,则|x-1+|x+2|有最小值吗?若有,请求出最小值,若没有,写出理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com