
ЁОЬтФПЁПЮЊбЁАЮгХаубЁЪжВЮМгбўКЃЧјЕкАЫНьЕТг§ЮФЛЏвеЪѕНкЁАЫаОЕфЁББШШќЛюЖЏЃЌОХФъМЖЃЈ1ЃЉЁЂЃЈ2ЃЉАрИљОнГѕШќГЩМЈЃЌИїбЁГі5УћбЁЪжВЮМгИДШќЃЌСНИіАрИїбЁГіЕФ5УћбЁЪжЕФИДШќГЩМЈШчЭМЫљЪО
ЃЈ1ЃЉИљОнЭМЪОЬюаДЯТБэ
АрМЖ | ЦНОљЪ§ЃЈЗжЃЉ | жаЮЛЪ§ЃЈЗжЃЉ | жкЪ§ЃЈЗжЃЉ |
ОХЃЈ1ЃЉ | 85 | ЁЁ ЁЁ | 85 |
ОХЃЈ2ЃЉ | ЁЁ ЁЁ | 80 | ЁЁ ЁЁ |
ЃЈ2ЃЉНсКЯСНАрИДШќГЩМЈЕФЦНОљЪ§КЭжаЮЛЪ§ЃЌЗжЮіФФИіАрМЖЕФИДШќГЩМЈНЯКУЃЛ
ЃЈ3ЃЉМЦЫуСНАрИДШќГЩМЈЕФЗНВюЃЌВЂЫЕУїФФИіАрЮхУћбЁЪжЕФГЩМЈНЯЮШЖЈЃЎ
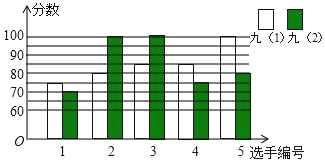
ЁОД№АИЁПЃЈ1ЃЉ
АрМЖ | ЦНОљЪ§ЃЈЗжЃЉ | жаЮЛЪ§ЃЈЗжЃЉ | жкЪ§ЃЈЗжЃЉ |
ОХЃЈ1ЃЉ | 85 | 85 | 85 |
ОХЃЈ2ЃЉ | 85 | 80 | 100 |
ЃЈ2ЃЉОХЃЈ1ЃЉАрГЩМЈКУаЉЃЛ
ЃЈ3ЃЉОХЃЈ1ЃЉАрЮхУћбЁЪжЕФГЩМЈНЯЮШЖЈЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙлВьЭМЗжБ№аДГіОХЃЈ1ЃЉАрКЭОХЃЈ2ЃЉАр5УћбЁЪжЕФИДШќГЩМЈЃЌШЛКѓИљОнжаЮЛЪ§ЕФЖЈвхКЭЦНОљЪ§ЕФЧѓЗЈвдМАжкЪ§ЕФЖЈвхЧѓНтМДПЩЃЛ
ЃЈ2ЃЉдкЦНОљЪ§ЯрЭЌЕФЧщПіЯТЃЌжаЮЛЪ§ИпЕФГЩМЈНЯКУЃЛ
ЃЈ3ЃЉИљОнЗНВюЙЋЪНМЦЫуМДПЩЃК![]() ЃЈПЩМђЕЅМЧвфЮЊЁАЕШгкВюЗНЕФЦНОљЪ§ЁБЃЉЃЎ
ЃЈПЩМђЕЅМЧвфЮЊЁАЕШгкВюЗНЕФЦНОљЪ§ЁБЃЉЃЎ
НтЃКЃЈ1ЃЉгЩЭМПЩжЊОХЃЈ1ЃЉАр5УћбЁЪжЕФИДШќГЩМЈЮЊЃК75ЁЂ80ЁЂ85ЁЂ85ЁЂ100ЃЌ
ЁрОХЃЈ1ЃЉЕФжаЮЛЪ§ЮЊ85ЃЌ
АбОХЃЈ2ЃЉЕФГЩМЈАДДгаЁЕНДѓЕФЫГађХХСаЮЊЃК70ЁЂ75ЁЂ80ЁЂ100ЁЂ100ЃЌ
ЁрОХЃЈ2ЃЉЕФЦНОљЪ§ЮЊЃЈ70+75+80+100+100ЃЉЁТ5ЃН85ЃЌ
ОХЃЈ2ЃЉАрЕФжкЪ§ЪЧ100ЃЛ
АрМЖ | ЦНОљЪ§ЃЈЗжЃЉ | жаЮЛЪ§ЃЈЗжЃЉ | жкЪ§ЃЈЗжЃЉ |
ОХЃЈ1ЃЉ | 85 | 85 | 85 |
ОХЃЈ2ЃЉ | 85 | 80 | 100 |
ЃЈ2ЃЉОХЃЈ1ЃЉАрГЩМЈКУаЉЃЎвђЮЊОХЃЈ1ЃЉАрЕФжаЮЛЪ§ИпЃЌЫљвдОХЃЈ1ЃЉАрГЩМЈКУаЉЃЎ
ЃЈ3ЃЉ![]() [ЃЈ75Љ85ЃЉ2+ЃЈ80Љ85ЃЉ2+ЃЈ85Љ85ЃЉ2+ЃЈ85Љ85ЃЉ2+ЃЈ100Љ85ЃЉ2]ЃН70ЃЌ
[ЃЈ75Љ85ЃЉ2+ЃЈ80Љ85ЃЉ2+ЃЈ85Љ85ЃЉ2+ЃЈ85Љ85ЃЉ2+ЃЈ100Љ85ЃЉ2]ЃН70ЃЌ
![]() [ЃЈ70Љ85ЃЉ2+ЃЈ100Љ85ЃЉ2+ЃЈ100Љ85ЃЉ2+ЃЈ75Љ85ЃЉ2+ЃЈ80Љ85ЃЉ2]ЃН160ЃЎ
[ЃЈ70Љ85ЃЉ2+ЃЈ100Љ85ЃЉ2+ЃЈ100Љ85ЃЉ2+ЃЈ75Љ85ЃЉ2+ЃЈ80Љ85ЃЉ2]ЃН160ЃЎ
Ёп![]() ЃЌ
ЃЌ
ЁрОХЃЈ1ЃЉАрЮхУћбЁЪжЕФГЩМЈНЯЮШЖЈЃЎ


 бєЙтПЮЬУПЮЪБзївЕЯЕСаД№АИ
бєЙтПЮЬУПЮЪБзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧхГЏЪ§бЇМвУЗЮФЖІЕФжјзїЁЖЗНГЬТлЁЗжагаетбљвЛЕРЬтЃКЩНЬяШ§ФЖЃЌГЁЕиСљФЖЃЌЙВелЪЕЬяЫФФЖЦпЗжЃЛгжЩНЬяЮхФЖЃЌГЁЕиШ§ФЖЃЌЙВелЪЕЬяЮхФЖЮхЗжЃЌЮЪУПФЖЩНЬяелЪЕЬяЖрЩйЃЌ
УПФЖГЁЕиелЪЕЬяЖрЩйЃП
выЮФЮЊЃКМйШчгаЩНЬя3ФЖЃЌГЁЕи6ФЖЃЌЦфВњСИЯрЕБгкЪЕЬя4.7ФЖЃЛгжЩНЬя5ФЖЃЌГЁЕи3ФЖЃЌЦфВњСИЯрЕБгкЪЕЬя5.5ФЖЃЌЮЪУПФЖЩНЬяКЭУПФЖГЁЕиВњСИИїЯрЕБгкЪЕЬяЖрЩйФЖЃПЧыФуНтД№ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуPЕФзјБъЮЊЃЈx1ЃЌy1ЃЉЃЌЕуQЕФзјБъЮЊЃЈx2ЃЌy2ЃЉЃЌЧвx1Ёйx2ЃЌy1Ёйy2ЃЎШєPЃЌQЮЊФГИіОиаЮЕФСНИіЖЅЕуЃЌЧвИУОиаЮЕФБпОљгыФГЬѕзјБъжсДЙжБЃЌдђГЦИУОиаЮЮЊЕуPЃЌQЕФЁАЯрЙиОиаЮЁБЃЌЯТЭМЂйЮЊЕуPЃЌQЕФЁАЯрЙиОиаЮЁБЕФЪОвтЭМЃЎ
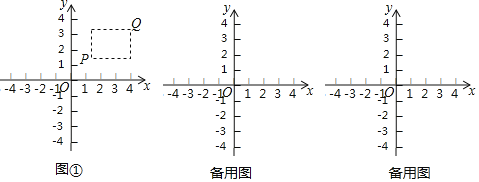
вбжЊЕуAЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌ
ЃЈ1ЃЉШєЕуBЕФзјБъЮЊЃЈ3ЃЌ1ЃЉЃЌЧѓЕуAЃЌBЕФЁАЯрЙиОиаЮЁБЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕуCдкжБЯпxЃН3ЩЯЃЌШєЕуAЃЌCЕФЁАЯрЙиОиаЮЁБЮЊе§ЗНаЮЃЌЧѓжБЯпACЕФБэДяЪНЃЛ
ЃЈ3ЃЉШєЕуDЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЃЌНЋжБЯпyЃН2x+bЦНвЦЃЌЕБЫќгыЕуAЃЌDЕФЁАЯрЙиОиаЮЁБУЛгаЙЋЙВЕуЪБЃЌЧѓГіbЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌABЃН![]() ЃЌADЃН2ЃЎЕуEЪЧBCБпЩЯЕФвЛИіЖЏЕуЃЌСЌНгAEЃЌЙ§ЕуDзїDFЁЭAEгкЕуFЃЎЕБЁїCDFЪЧЕШбќШ§НЧаЮЪБЃЌBEЕФГЄЮЊ_____ЃЎ
ЃЌADЃН2ЃЎЕуEЪЧBCБпЩЯЕФвЛИіЖЏЕуЃЌСЌНгAEЃЌЙ§ЕуDзїDFЁЭAEгкЕуFЃЎЕБЁїCDFЪЧЕШбќШ§НЧаЮЪБЃЌBEЕФГЄЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГаЁЧјгавЛПщГЄЮЊ30mЃЌПэЮЊ24mЕФОиаЮПеЕиЃЌМЦЛЎдкЦфжааоНЈСНПщЯрЭЌЕФОиаЮТЬЕиЃЌЫќУЧЕФУцЛ§жЎКЭЮЊ480m2ЃЌСНПщТЬЕижЎМфМАжмБпгаПэЖШЯрЕШЕФШЫааЭЈЕРЃЌдђШЫааЭЈЕРЕФПэЖШЮЊЖрЩйУзЃП
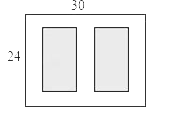
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПН№ЬУЦяздааГЕТУаадНРДдНЪмЕНШЫУЧЕФЯВАЎЃЌИїжжЦЗХЦЕФЩНЕиздааГЕЯрМЬЭЖЗХЪаГЁЃЌФГГЕааОгЊЕФAаЭГЕШЅФъ2дТЗнЯњЪлзмЖюЮЊ3.2ЭђдЊЃЌНёФъОЙ§ИФдьЩ§МЖКѓAаЭГЕУПСОЯњЪлМлБШШЅФъдіМг400дЊЃЌШєНёФъ2дТЗнгыШЅФъ2дТЗнТєГіЕФAаЭГЕЪ§СПЯрЭЌЃЌдђНёФъ2дТЗнAаЭГЕЯњЪлзмЖюНЋБШШЅФъ2дТЗнЯњЪлзмЖюдіМг25%ЃЎ
ЃЈ1ЃЉЧѓНёФъ2дТЗнAаЭГЕУПСОЯњЪлМлЖрЩйдЊЃП
ЃЈ2ЃЉИУГЕааМЦЛЎНёФъ3дТЗнаТНјвЛХњAаЭГЕКЭBаЭГЕЙВ50СОЃЌЧвBаЭГЕЕФНјЛѕЪ§СПВЛГЌЙ§AаЭГЕЪ§СПЕФ2БЖЃЌAЁЂBСНжжаЭКХГЕЕФНјЛѕКЭЯњЪлМлИёШчЯТБэЃЌЮЪгІШчКЮНјЛѕВХФмЪЙетХњГЕЛёРћзюЖрЃПЁЁ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЁЯABCЕФЦНЗжЯпНЛADгкЕуEЃЌЙ§ЕуDзїBEЕФЦНааЯпНЛгкBCгкFЃЎ
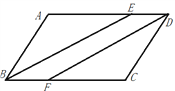
ЃЈ1ЃЉЧѓжЄЃКЁїABEЁеЁїCDFЃЛ
ЃЈ2ЃЉШєAB=6ЃЌBC=8ЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
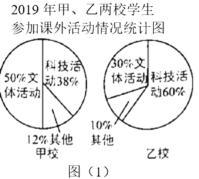
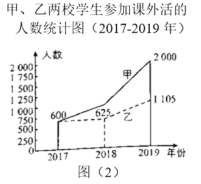
ЁОЬтФПЁПЯТУцСНЗљЭГМЦЭМШчЭМЃЈ1ЃЉЁЂЭМЃЈ2ЃЉЗДгГСЫФГЪаМзЁЂввСНаЃбЇЩњВЮМгПЮЭтЛюЖЏЕФЧщПіЁЃЧыФуЭЈЙ§ЭМжааХЯЂЛиД№ЯТУцЕФЮЪЬт.
ЃЈ1ЃЉЭЈЙ§ЖдЭМЃЈ1ЃЉЕФЗжЮіЃЌаДГівЛЬѕФуШЯЮЊе§ШЗЕФНсТлЃЛ
ЃЈ2ЃЉЭЈЙ§ЖдЭМЃЈ2ЃЉЕФЗжЮіЃЌаДГівЛЬѕФуШЯЮЊе§ШЗЕФНсТлЃЛ
ЃЈ3ЃЉ2019ФъМзЁЂввСНаЃВЮМгПЦММЛюЖЏЕФбЇЩњШЫЪ§ЙВгаЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪпВЫжжжВЛљЕиЮЊЬсИпЪпВЫВњСПЃЌМЦЛЎЖдМзЁЂввСНжжаЭКХЪпВЫДѓХяНјааИФдьЃЌИљОндЄЫуЃЌИФдь2ИіМзжжаЭКХДѓХяБШ1ИіввжжаЭКХДѓХяЖрашзЪН№6ЭђдЊЃЌИФдь1ИіМзжжаЭКХДѓХяКЭ2ИіввжжаЭКХДѓХяЙВашзЪН№48ЭђдЊЃЎ
ЃЈ1ЃЉИФдь1ИіМзжжаЭКХКЭ1ИіввжжаЭКХДѓХяЫљашзЪН№ЗжБ№ЪЧЖрЩйЭђдЊЃП
ЃЈ2ЃЉвбжЊИФдь1ИіМзжжаЭКХДѓХяЕФЪБМфЪЧ5ЬьЃЌИФдь1ИіввжжаЭКХДѓИХЕФЪБМфЪЧ3ЬьЃЌИУЛљЕиМЦЛЎИФдьМзЁЂввСНжжЪпВЫДѓХяЙВ8ИіЃЌИФдьзЪН№зюЖрФмЭЖШы128ЭђдЊЃЌвЊЧѓИФдьЪБМфВЛГЌЙ§35ЬьЃЌЧыЮЪгаМИжжИФдьЗНАИЃПФФжжЗНАИЛљЕиЭЖШызЪН№зюЩйЃЌзюЩйЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com